
【題目】對于兩個定義域均為D的函數f(x),g(x),若存在最小正實數M,使得對于任意x∈D,都有|f(x)-g(x)|≤M,則稱M為函數f(x),g(x)的“差距”,并記作||f(x),g(x)||.
(1)求f(x)=sinx(x∈R),g(x)=cosx(x∈R)的差距;
(2)設f(x)=![]() (x∈[1,
(x∈[1,![]() ]),g(x)=mlnx (x∈[1,
]),g(x)=mlnx (x∈[1,![]() ]).(e≈2.718)
]).(e≈2.718)
①若m=2,且||f(x),g(x)||=1,求滿足條件的最大正整數a;
②若a=2,且||f(x),g(x)||=2,求實數m的取值范圍.
【答案】(1)![]() (2) ①3.②{
(2) ①3.②{![]() -2,
-2,![]() +2}.
+2}.
【解析】
試題(1)由定義知求|sinx-cosx|最大值,根據三角函數配角公式得|sinx-cosx|=![]() |sin(x-
|sin(x-![]() )|≤
)|≤![]() ,所以差距為
,所以差距為![]() (2) ①根據定義先研究函數h(x)=f(x)-g(x)=
(2) ①根據定義先研究函數h(x)=f(x)-g(x)=![]() -2lnx單調性:(0,16)上單調減,(16,+∞)上單調增,因為h(1)=1,所以h(
-2lnx單調性:(0,16)上單調減,(16,+∞)上單調增,因為h(1)=1,所以h(![]() )
)![]() -1,因此
-1,因此![]() ②由定義得
②由定義得![]() -mlnx|≤2恒成立,利用變量分離法得
-mlnx|≤2恒成立,利用變量分離法得![]() 對x∈(1,e]恒成立,分別利用導數求函數w(x)=
對x∈(1,e]恒成立,分別利用導數求函數w(x)=![]() 最小值及函數v(x)=
最小值及函數v(x)=![]() 最大值即可
最大值即可
試題解析:(1)|f(x)-g(x)|=|sinx-cosx|=![]() |sin(x-
|sin(x-![]() )|≤
)|≤![]() ,當x=kπ+
,當x=kπ+![]() ,k∈Z時取“=”,所以||f(x),g(x)||=
,k∈Z時取“=”,所以||f(x),g(x)||=![]()
(2)①令h(x)=f(x)-g(x)=![]() -2lnx.則h′(x)=
-2lnx.則h′(x)=![]() ,令h′(x)=0,則x=16.列表:
,令h′(x)=0,則x=16.列表:
x | (0,16) | 16 | (16,+∞) |
h′(x) | - | 0 | + |
h(x) | ↘ | ↗ |
∵h(1)=1;當a=3時,h(![]() )=
)=![]() -3,由于
-3,由于![]() >16,因此
>16,因此![]() >2,所以
>2,所以![]() -3>-1;
-3>-1;
當a=4時,h(![]() )=e-4<-1,故滿足條件的最大正整數為3.
)=e-4<-1,故滿足條件的最大正整數為3.
②法一:由a=2,且||f(x),g(x)||=2,得|f(x)-g(x)|≤2,從而|![]() -mlnx|≤2,所以-2≤
-mlnx|≤2,所以-2≤![]() -mlnx≤2.
-mlnx≤2.
當x=1時,上式顯然成立;
當x∈(1,e]時,上式化為![]()
令w(x)=![]() ,則w′(x)=
,則w′(x)=![]() <0,
<0,
從而w(x)在(1,e]上遞減,從而w(x)min=w(e)=![]() +2,從而m≤
+2,從而m≤![]() +2;
+2;
令v(x)=![]() ,則v′(x)=
,則v′(x)=![]() >0,
>0,
從而v(x)在(1,e]上遞增,從而v(x)max=v(e)=![]() -2,從而m≥
-2,從而m≥![]() -2,
-2,
所以![]() -2≤m≤
-2≤m≤![]() +2
+2
又由于||f(x),g(x)||=2,故m=![]() -2或m=
-2或m=![]() +2,所以m的取值范圍為{
+2,所以m的取值范圍為{![]() -2,
-2,![]() +2}.
+2}.
法二:令h(x)=f(x)-g(x)=![]() -mlnx,則h′(x)=
-mlnx,則h′(x)=![]() .
.
(1)若m≤![]() ,則h′(x)≥0,從而h(x)在[1,e]上遞增,又h(1)=1,h(e)=
,則h′(x)≥0,從而h(x)在[1,e]上遞增,又h(1)=1,h(e)=![]() -m,所以
-m,所以![]() -m=2,m=
-m=2,m=![]() -2;
-2;
(ii)若m≥![]() ,則h′(x)≤0,從而h(x)在[1,e]上遞減,又h(1)=1,h(e)=
,則h′(x)≤0,從而h(x)在[1,e]上遞減,又h(1)=1,h(e)=![]() -m,所以
-m,所以![]() -m=-2,m=
-m=-2,m=![]() -2;
-2;
(iii)若![]() <m<
<m<![]() ,則由h′(x)=0,可得x=4m2,列表
,則由h′(x)=0,可得x=4m2,列表
x | 1 | (1, 4m2) | 4m2 | (4m2,e) | e |
h′(x) | - | 0 | + | ||
h(x) | 1 | ↘ | 2m-mln(4m2) | ↗ |
|
因為![]() -m<
-m<![]() -<2,所以2m-mln(4m2)=-2,.
-<2,所以2m-mln(4m2)=-2,.
令u(m)=2m-mln(4m2)=m(2-ln4)-2mlnm
∴u′(m)=2-ln4-2-2lnm=-ln4-2lnm=-2 ln2m<0,
∴u(m)>u(![]() )=
)=![]() -
-![]() =
=![]() ,故該情況不成立.
,故該情況不成立.
綜上,m的取值范圍是{![]() -2,
-2,![]() +2}.
+2}.


 口算能手系列答案
口算能手系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中曲線
中曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以
為參數),以![]() 為極點,
為極點,![]() 軸的正半軸為極軸,建立極坐標系,直線
軸的正半軸為極軸,建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程以及直線
的普通方程以及直線![]() 的直角坐標方程;
的直角坐標方程;
(2)將曲線![]() 向左平移2個單位,再將曲線
向左平移2個單位,再將曲線![]() 上的所有點的橫坐標縮短為原來的
上的所有點的橫坐標縮短為原來的![]() ,得到曲線
,得到曲線![]() ,求曲線
,求曲線![]() 上的點到直線
上的點到直線![]() 的距離的最小值.
的距離的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義:從數列{an}中抽取m(m∈N,m≥3)項按其在{an}中的次序排列形成一個新數列{bn},則稱{bn}為{an}的子數列;若{bn}成等差(或等比),則稱{bn}為{an}的等差(或等比)子數列.
(1)記數列{an}的前n項和為Sn,已知![]() .
.
①求數列{an}的通項公式;
②數列{an}是否存在等差子數列,若存在,求出等差子數列;若不存在,請說明理由.
(2)已知數列{an}的通項公式為an=n+a(a∈Q+),證明:{an}存在等比子數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,橢圓
中,橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,左、右頂點分別為
,左、右頂點分別為![]() 、
、![]() ,線段
,線段![]() 的長為4.點
的長為4.點![]() 在橢圓
在橢圓![]() 上且位于第一象限,過點
上且位于第一象限,過點![]() ,
,![]() 分別作
分別作![]() ,
,![]() ,直線
,直線![]() ,
,![]() 交于點
交于點![]() .
.
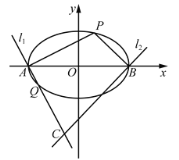
(1)若點![]() 的橫坐標為-1,求點
的橫坐標為-1,求點![]() 的坐標;
的坐標;
(2)直線![]() 與橢圓
與橢圓![]() 的另一交點為
的另一交點為![]() ,且
,且![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某籃球隊員進行定點投籃訓練,每次投中的概率是![]() ,且每次投籃的結果互不影響.
,且每次投籃的結果互不影響.
(1)假設這名隊員投籃5次,求恰有2次投中的概率;
(2)假設這名隊員投籃3次,每次投籃,投中得1分,為投中得0分,在3次投籃中,若有2次連續投中,而另外一次未投中,則額外加1分;若3次全投中,則額外加3分,記![]() 為隊員投籃3次后的總的分數,求
為隊員投籃3次后的總的分數,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 是定義在R上的奇函數,當
是定義在R上的奇函數,當![]() 時,
時,![]() ,給出下列命題:
,給出下列命題:
①當![]() 時,
時,![]() ;
;
②函數![]() 有2個零點;
有2個零點;
③![]() 的解集為
的解集為![]() ;
;
④![]() ,
,![]() ,都有
,都有![]() .
.
其中真命題的個數為( )
A.4B.3C.2D.1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC的內角A,B,C所對邊分別為a、b、c,且2acosC=2b-c.
(1)求角A的大小;
(2)若AB=3,AC邊上的中線SD的長為![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】人們隨著生活水平的提高,健康意識逐步加強,健身開始走進人們生活,在健身方面投入越來越多,為了調查參與健身的年輕人一年健身的花費情況,研究人員在![]() 地區隨機抽取了參加健身的青年男性、女性各50名,將其花費統計情況如下表所示:
地區隨機抽取了參加健身的青年男性、女性各50名,將其花費統計情況如下表所示:
分組(花費) | 頻數 |
| 6 |
| 22 |
| 25 |
| 35 |
| 8 |
| 4 |
男性 | 女性 | 合計 | |
健身花費不超過2400元 | 23 | ||
健身花費超過2400元 | 20 | ||
合計 |
(1)完善二聯表中的數據;
(2)根據表中的數據情況,判斷是否有99%的把握認為健身的花費超過2400元與性別有關;
(3)求這100名被調查者一年健身的平均花費(同一組數據用該區間的中點值代替).
附:![]()
P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.01 |
k | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com