
【題目】如圖,傾斜角為a的直線經過拋物線![]() 的焦點F,且與拋物線交于A、B兩點.
的焦點F,且與拋物線交于A、B兩點.
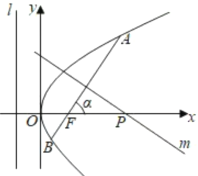
(1)求拋物線的焦點F的坐標及準線![]() 的方程;
的方程;
(2)若a為銳角,作線段AB的垂直平分線m交x軸于點P,證明|FP|-|FP|cos2a為定值,并求此定值.
【答案】(1)![]() (2)8
(2)8
【解析】
試題(1)根據(jù)拋物線的標準方程,可求拋物線的焦點F的坐標及準線l的方程;(2)作AC⊥l,BD⊥l,垂足為C,D,求出|FA|,|FB|,即可得到結論
試題解析:(1)解:設拋物線的標準方程為![]() ,則
,則![]() ,從而
,從而![]() 因此焦點
因此焦點![]() 的坐標為(2,0).又準線方程的一般式為
的坐標為(2,0).又準線方程的一般式為![]() .從而所求準線l的方程為
.從而所求準線l的方程為![]() .
.
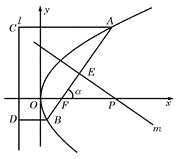
(2)解法一:如圖(21)圖作AC⊥l,BD⊥l,垂足為C、D,則由拋物線的定義知|FA|=|AC|,|FB|=|BD|.
記A的橫坐標別為xx,則|FA|=|AC|=![]() 解得
解得![]() ,
,
類似地有![]() ,解得
,解得![]() .
.
記直線m與AB的交點為E,則
![]() ,
,
所以![]() .故
.故![]() .
.
解法二:設![]() ,
,![]() ,直線AB的斜率為
,直線AB的斜率為![]() ,則直線方程為
,則直線方程為![]() .
.
將此式代入![]() ,得
,得![]() ,故
,故![]() .
.
記直線m與AB的交點為![]() ,則
,則
![]() ,
,![]() ,故直線m的方程為
,故直線m的方程為![]() .
.
令y=0,得P的橫坐標![]() 故
故![]() .
.
從而![]() 為定值.
為定值.


科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)列![]() 和
和![]() 滿足:
滿足:![]() ,
,![]() ,
,![]() 且對一切
且對一切![]() ,均有
,均有![]() .
.
(1)求證:數(shù)列![]() 為等差數(shù)列,并求數(shù)列
為等差數(shù)列,并求數(shù)列![]() 的通項公式;
的通項公式;
(2)求數(shù)列![]() 的前
的前![]() 項和
項和![]() ;
;
(3)設![]() ,記數(shù)列
,記數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,求正整數(shù)
,求正整數(shù)![]() ,使得對任意
,使得對任意![]() ,均有
,均有![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】等差數(shù)列![]() 首項和公差都是
首項和公差都是![]() ,記
,記![]() 的前n項和為
的前n項和為![]() ,等比數(shù)列
,等比數(shù)列![]() 各項均為正數(shù),公比為q,記
各項均為正數(shù),公比為q,記![]() 的前n項和為
的前n項和為![]() :
:
(1)寫出![]()
![]() 構成的集合A;
構成的集合A;
(2)若將![]() 中的整數(shù)項按從小到大的順序構成數(shù)列
中的整數(shù)項按從小到大的順序構成數(shù)列![]() ,求
,求![]() 的一個通項公式;
的一個通項公式;
(3)若q為正整數(shù),問是否存在大于1的正整數(shù)k,使得![]()
![]() 同時為(1)中集合A的元素?若存在,寫出所有符合條件的
同時為(1)中集合A的元素?若存在,寫出所有符合條件的![]() 的通項公式,若不存在,請說明理由.
的通項公式,若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知正項數(shù)列![]() ,
,![]() 滿足:對任意正整數(shù)
滿足:對任意正整數(shù)![]() ,都有
,都有![]() ,
,![]() ,
,![]() 成等差數(shù)列,
成等差數(shù)列,![]() ,
,![]() ,
,![]() 成等比數(shù)列,且
成等比數(shù)列,且![]() ,
,![]() .
.
(Ⅰ)求證:數(shù)列![]() 是等差數(shù)列;
是等差數(shù)列;
(Ⅱ)求數(shù)列![]() ,
,![]() 的通項公式;
的通項公式;
(Ⅲ)設![]() =
=![]() +
+![]() +…+
+…+![]() ,如果對任意的正整數(shù)
,如果對任意的正整數(shù)![]() ,不等式
,不等式![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,已知曲線![]() ,曲線
,曲線![]() ,P是平面上一點,若存在過點P的直線與
,P是平面上一點,若存在過點P的直線與![]() 都有公共點,則稱P為“C1—C2型點”.
都有公共點,則稱P為“C1—C2型點”.
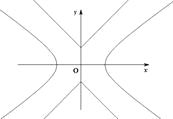
(1)在正確證明![]() 的左焦點是“C1—C2型點”時,要使用一條過該焦點的直線,試寫出一條這樣的直線的方程(不要求驗證);
的左焦點是“C1—C2型點”時,要使用一條過該焦點的直線,試寫出一條這樣的直線的方程(不要求驗證);
(2)設直線![]() 與
與![]() 有公共點,求證
有公共點,求證![]() ,進而證明原點不是“C1—C2型點”;
,進而證明原點不是“C1—C2型點”;
(3)求證:圓![]() 內的點都不是“C1—C2型點”.
內的點都不是“C1—C2型點”.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】若無窮數(shù)列![]() 滿足:只要
滿足:只要![]() ,必有
,必有![]() ,則稱
,則稱![]() 具有性質
具有性質![]() .
.
(1)若![]() 具有性質
具有性質![]() ,且
,且![]()
![]() ,求
,求![]() ;
;
(2)若無窮數(shù)列![]() 是等差數(shù)列,無窮數(shù)列
是等差數(shù)列,無窮數(shù)列![]() 是等比數(shù)列,
是等比數(shù)列,![]() ,
,![]() ,
,![]() .判斷
.判斷![]() 是否具有性質
是否具有性質![]() ,并說明理由;
,并說明理由;
(3)設![]() 是無窮數(shù)列,已知
是無窮數(shù)列,已知![]() .求證:“對任意
.求證:“對任意![]() 都具有性質
都具有性質![]() ”的充要條件為“
”的充要條件為“![]() 是常數(shù)列”.
是常數(shù)列”.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】(本題12分)已知![]() 且
且![]() ,函數(shù)
,函數(shù)![]() ,
, ![]() ,
,
記![]()
(1)求函數(shù)![]() 的定義域
的定義域![]() 及其零點;
及其零點;
(2)若關于![]() 的方程
的方程![]() 在區(qū)間
在區(qū)間![]() 內僅有一解,求實數(shù)
內僅有一解,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知![]() 、
、![]() 為橢圓
為橢圓![]() (
(![]() )和雙曲線
)和雙曲線![]() 的公共頂點,
的公共頂點,![]() 、
、![]() 分為雙曲線和橢圓上不同于
分為雙曲線和橢圓上不同于![]() 、
、![]() 的動點,且滿足
的動點,且滿足![]() ,設直線
,設直線![]() 、
、![]() 、
、![]() 、
、![]() 的斜率分別為
的斜率分別為![]() 、
、![]() 、
、![]() 、
、![]() .
.
(1)求證:點![]() 、
、![]() 、
、![]() 三點共線;
三點共線;
(2)求![]() 的值;
的值;
(3)若![]() 、
、![]() 分別為橢圓和雙曲線的右焦點,且
分別為橢圓和雙曲線的右焦點,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】當前,以“立德樹人”為目標的課程改革正在有序推進. 高中聯(lián)招對初三畢業(yè)學生進行體育測試,是激發(fā)學生、家長和學校積極開展體育活動,保證學生健康成長的有效措施. 某地區(qū)2018年初中畢業(yè)生升學體育考試規(guī)定,考生必須參加立定跳遠、擲實心球、1分鐘跳繩三項測試,三項考試滿分為50分,其中立定跳遠15分,擲實心球15分,1分鐘跳繩20分. 某學校在初三上學期開始時要掌握全年級學生每分鐘跳繩的情況,隨機抽取了100名學生進行測試,得到右邊頻率分布直方圖,且規(guī)定計分規(guī)則如下表:
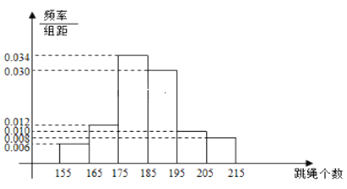

(1)現(xiàn)從樣本的100名學生中,任意選取2人,求兩人得分之和不大于33分的概率;
(2)若該校初三年級所有學生的跳繩個數(shù)![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,用樣本數(shù)據(jù)的平均值和方差估計總體的期望和方差,已知樣本方差
,用樣本數(shù)據(jù)的平均值和方差估計總體的期望和方差,已知樣本方差![]() (各組數(shù)據(jù)用中點值代替). 根據(jù)往年經驗,該校初三年級學生經過一年的訓練,正式測試時每人每分鐘跳繩個數(shù)都有明顯進步,假設今年正式測試時每人每分鐘跳繩個數(shù)比初三上學期開始時個數(shù)增加10個,現(xiàn)利用所得正態(tài)分布模型:
(各組數(shù)據(jù)用中點值代替). 根據(jù)往年經驗,該校初三年級學生經過一年的訓練,正式測試時每人每分鐘跳繩個數(shù)都有明顯進步,假設今年正式測試時每人每分鐘跳繩個數(shù)比初三上學期開始時個數(shù)增加10個,現(xiàn)利用所得正態(tài)分布模型:
(ⅰ)預估全年級恰好有2000名學生時,正式測試每分鐘跳182個以上的人數(shù);(結果四舍五入到整數(shù))
(ⅱ)若在全年級所有學生中任意選取3人,記正式測試時每分鐘跳195個以上的人數(shù)為![]() ,求隨機變量
,求隨機變量![]() 的分布列和期望. 附:若隨機變量
的分布列和期望. 附:若隨機變量![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com