
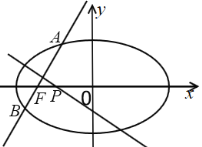
【題目】已知橢圓![]() (
(![]() )的上頂點為
)的上頂點為![]() ,左焦點為
,左焦點為![]() ,離心率為
,離心率為![]() ,直線
,直線![]() 與圓
與圓![]() 相切.
相切.

(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設過點![]() 且斜率存在的直線
且斜率存在的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,線段
兩點,線段![]() 的垂直平分線交
的垂直平分線交![]() 軸于點
軸于點![]() ,試判斷
,試判斷![]() 是否為定值?并說明理由.
是否為定值?并說明理由.
【答案】(1)![]() ;(2)存在,定值
;(2)存在,定值![]() ,理由見解析
,理由見解析
【解析】
(1)根據已知條件得![]() ,
,![]() ,再由直線與圓相切時,圓心到直線的距離等于半徑可求得
,再由直線與圓相切時,圓心到直線的距離等于半徑可求得![]() ,得出橢圓
,得出橢圓![]() 的標準方程;
的標準方程;
(2)設![]() ,
,![]() ,
,![]() ,設直線
,設直線![]() ,聯立
,聯立 ,消去
,消去![]() 得
得![]() ,
,![]() ,
,![]() ,根據弦長公式求
,根據弦長公式求![]() ,
,
法一:由![]() 在線段
在線段![]() 的垂直平分線上,得
的垂直平分線上,得![]() ,由兩點的距離公式和橢圓的標準方程可得出中點的橫坐標
,由兩點的距離公式和橢圓的標準方程可得出中點的橫坐標![]() ,可求得
,可求得![]() ,可得所求的比值;
,可得所求的比值;
法二:求出 線段![]() 的中點和線段
的中點和線段![]() 的垂直平分線方程,可得點
的垂直平分線方程,可得點![]() 的坐標,可求得
的坐標,可求得![]() ,可得所求的比值;
,可得所求的比值;
(1)如圖,![]() ,
,![]() ,
,![]() ,直線
,直線![]() 的方程為
的方程為![]() ,
,
![]() 直線
直線![]() 與圓
與圓![]() 相切,
相切,![]() ,
,![]() ,
,
![]() 橢圓
橢圓![]() 的標準方程為
的標準方程為![]() .
.
(2)設![]() ,
,![]() ,
,![]() ,
,
設直線![]() ,聯立
,聯立 ,消去
,消去![]() 得
得![]() ,
,
![]() ,
,![]()
![]()
法一:![]() 在線段
在線段![]() 的垂直平分線上,
的垂直平分線上,![]() ,
,![]() ………①
………①
![]() 在橢圓
在橢圓![]() 上,
上,![]() ,
,![]() ,
,
代入①得![]() ,化簡得
,化簡得![]()
![]()
法二: 線段![]() 的中點為
的中點為![]() ,
,![]() 線段
線段![]() 的垂直平分線為
的垂直平分線為![]() ,
,
令![]() ,得
,得![]()
![]() ,
,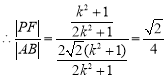 ,
,
故![]() 為定值
為定值![]() .
.



 天天向上口算本系列答案
天天向上口算本系列答案科目:高中數學 來源: 題型:
【題目】設![]() ,
,![]() 為正整數,一個正整數數列
為正整數,一個正整數數列![]() 滿足
滿足![]() .對
.對![]() ,定義集合
,定義集合![]() .數列
.數列![]() 中的
中的![]() 是集合
是集合![]() 中元素的個數.
中元素的個數.
(1)若數列![]() 為5,3,3,2,1,1,寫出數列
為5,3,3,2,1,1,寫出數列![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 為公比為
為公比為![]() 的等比數列,求
的等比數列,求![]() ;
;
(3)對![]() ,定義集合
,定義集合![]() ,令
,令![]() 是集合
是集合![]() 中元素數的個數.求證:對
中元素數的個數.求證:對![]() ,均有
,均有![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 是無窮數列,滿足
是無窮數列,滿足![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)求證:“數列![]() 中存在
中存在![]() 使得
使得![]() ”是“數列
”是“數列![]() 中有無數多項是
中有無數多項是![]() ”的充要條件;
”的充要條件;
(3)求證:在數列![]() 中
中![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() (其中
(其中![]() 為常數).
為常數).
(1)如果函數![]() 和
和![]() 有相同的極值點,求
有相同的極值點,求![]() 的值;
的值;
(2)當![]() ,
,![]() 恒成立,求
恒成立,求![]() 的取值范圍;
的取值范圍;
(3)記函數![]() ,若函數
,若函數![]() 有
有![]() 個不同的零點,求實數
個不同的零點,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,直線l的參數方程為![]() ,(t為參數),在以坐標原點為極點,x軸正半軸為極軸的極坐標系中,曲線C1:ρ=2cosθ,
,(t為參數),在以坐標原點為極點,x軸正半軸為極軸的極坐標系中,曲線C1:ρ=2cosθ,![]() .
.
(1)求C1與C2交點的直角坐標;
(2)若直線l與曲線C1,C2分別相交于異于原點的點M,N,求|MN|的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代典籍《周易》用“卦”描述萬物的變化,每一卦由六組成.其中記載一種起卦方法稱為“大衍法”,其做法為:從50根草中先取出一根放在案上顯著位置,用這根蓍草象征太極.將剩下的49根隨意分成左右兩份,然后從右邊拿出一根放中間,再把左右兩份每4根一數,直到兩份中最后各剩下不超過4根(含4根)為止,把兩份剩下的也放中間.將49根里除中間之外的蓍草合在一起,為一變;重復一變的步驟得二變和三變,三變得一爻.若一變之后還剩40根蓍草,則二變之后還剩36根蓍草的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】十九大以來,某貧困地區扶貧辦積極貫徹落實國家精準扶貧的政策要求,帶領廣大農村地區人民群眾脫貧奔小康。經過不懈的奮力拼搏,新農村建設取得巨大進步,農民年收入也逐年增加。為了更好的制定2019年關于加快提升農民年收人力爭早日脫貧的工作計劃,該地扶貧辦統計了2018年![]() 位農民的年收人并制成如下頻率分布直方圖:
位農民的年收人并制成如下頻率分布直方圖:
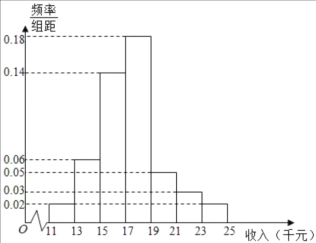
(1)根據頻率分布直方圖,估計![]() 位農民的年平均收入
位農民的年平均收入![]() (單位:千元)(同一組數據用該組數據區間的中點值表示);
(單位:千元)(同一組數據用該組數據區間的中點值表示);
(2)由頻率分布直方圖,可以認為該貧困地區農民年收入![]() 服從正態分布
服從正態分布![]() ,其中
,其中![]() 近似為年平均收入
近似為年平均收入![]() ,
,![]() 近似為樣本方差
近似為樣本方差![]() ,經計算得
,經計算得![]() .利用該正態分布,求:
.利用該正態分布,求:
(i)在2019年脫貧攻堅工作中,若使該地區約有占總農民人數的![]() 的農民的年收入高于扶貧辦制定的最低年收入標準,則最低年收入大約為多少千元?
的農民的年收入高于扶貧辦制定的最低年收入標準,則最低年收入大約為多少千元?
(ii)為了調研“精準扶貧,不落一人”的政策要求落實情況,扶貧辦隨機走訪了![]() 位農民。若每個農民的年收人相互獨立,問:這
位農民。若每個農民的年收人相互獨立,問:這![]() 位農民中的年收入不少于
位農民中的年收入不少于![]() 千元的人數最有可能是多少?
千元的人數最有可能是多少?
附:參考數據與公式![]()
則①![]() ;②
;②![]() ;③
;③![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市環保部門對市中心每天的環境污染情況進行調查研究后,發現一天中環境綜合污染指數![]() 與時刻
與時刻![]() (時)的關系為
(時)的關系為![]() ,
,![]() ,其中
,其中![]() 是與氣象有關的參數,且
是與氣象有關的參數,且![]() .若用每天
.若用每天![]() 的最大值為當天的綜合污染指數,并記作
的最大值為當天的綜合污染指數,并記作![]() .
.
(1)令![]() ,
,![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(2)求![]() 的表達式,并規定當
的表達式,并規定當![]() 時為綜合污染指數不超標,求當
時為綜合污染指數不超標,求當![]() 在什么范圍內時,該市市中心的綜合污染指數不超標.
在什么范圍內時,該市市中心的綜合污染指數不超標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,設拋物線![]() 與
與![]() 的公共點
的公共點![]() 的橫坐標為
的橫坐標為![]() ,過
,過![]() 且與
且與![]() 相切的直線交
相切的直線交![]() 于另一點
于另一點![]() ,過
,過![]() 且與
且與![]() 相切的直線交
相切的直線交![]() 于另一點
于另一點![]() ,記
,記![]() 為
為![]() 的面積.
的面積.
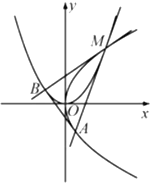
(Ⅰ)求![]() 的值(用
的值(用![]() 表示);
表示);
(Ⅱ)若![]() ,求
,求![]() 的取值范圍.
的取值范圍.
注:若直線與拋物線有且只有一個公共點,且與拋物線的對稱軸不平行也不重合,則稱該直線與拋物線相切.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com