
【題目】數(shù)列![]() 中,
中,![]() 在直線
在直線![]() .
.
(1)求數(shù)列{an}的通項(xiàng)公式;
(2)令![]() ,數(shù)列
,數(shù)列![]() 的前n項(xiàng)和為
的前n項(xiàng)和為![]() .
.
(ⅰ)求![]() ;
;
(ⅱ)是否存在整數(shù)λ![]() ,使得不等式(-1)nλ<
,使得不等式(-1)nλ<![]() (n∈N
(n∈N![]() )恒成立?若存在,求出λ的取值的集合;若不存在,請(qǐng)說(shuō)明理由.
)恒成立?若存在,求出λ的取值的集合;若不存在,請(qǐng)說(shuō)明理由.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由題意結(jié)合等差數(shù)列的定義可知數(shù)列![]() 為等差數(shù)列,公差為
為等差數(shù)列,公差為![]() ,據(jù)此求解其通項(xiàng)公式即可;
,據(jù)此求解其通項(xiàng)公式即可;
(2)(ⅰ)由題意可得![]() ,然后裂項(xiàng)求和確定其前n項(xiàng)和即可.
,然后裂項(xiàng)求和確定其前n項(xiàng)和即可.
(ⅱ)由題意分類討論![]() 為奇數(shù)和
為奇數(shù)和![]() 為偶數(shù)兩種情況可得
為偶數(shù)兩種情況可得![]() 取值集合為
取值集合為![]() .
.
(1)因?yàn)?/span>![]() ,
,![]() 在直線
在直線![]() ,
,
所以![]() ,即數(shù)列
,即數(shù)列![]() 為等差數(shù)列,公差為
為等差數(shù)列,公差為![]() ,
,
所以![]() -1.
-1.
(2)(ⅰ)![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
(ⅱ)存在整數(shù)![]() 使得不等式
使得不等式![]() (n∈N
(n∈N![]() )恒成立.
)恒成立.
因?yàn)?/span>![]() =
=![]() .
.
要使得不等式![]() (n∈N
(n∈N![]() )恒成立,應(yīng)有:
)恒成立,應(yīng)有:
當(dāng)![]() 為奇數(shù)時(shí),
為奇數(shù)時(shí),![]() ,即
,即![]() -
-![]() .
.
所以當(dāng)![]() 時(shí),
時(shí),![]() 的最大值為-
的最大值為-![]() ,所以只需
,所以只需![]() -
-![]() .
.
當(dāng)![]() 為偶數(shù)時(shí),
為偶數(shù)時(shí),![]() ,
,
所以當(dāng)![]() 時(shí),
時(shí),![]() 的最小值為
的最小值為![]() ,所以只需
,所以只需![]() .
.
可知存在![]() ,且
,且![]() .
.
又![]() 為整數(shù),所以
為整數(shù),所以![]() 取值集合為
取值集合為![]() .
.


 口算心算速算應(yīng)用題系列答案
口算心算速算應(yīng)用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知公差不為零的等差數(shù)列{an}中, S2=16,且![]() 成等比數(shù)列.
成等比數(shù)列.
(1)求數(shù)列{an}的通項(xiàng)公式;
(2)求數(shù)列{|an|}的前n項(xiàng)和Tn.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】“雙十一網(wǎng)購(gòu)狂歡節(jié)”源于淘寶商城(天貓)2009年11月11 日舉辦的促銷活動(dòng),當(dāng)時(shí)參與的商家數(shù)量和促銷力度均有限,但營(yíng)業(yè)額遠(yuǎn)超預(yù)想的效果,于是11月11日成為天貓舉辦大規(guī)模促銷活動(dòng)的固定日期.如今,中國(guó)的“雙十一”已經(jīng)從一個(gè)節(jié)日變成了全民狂歡的“電商購(gòu)物日”.某淘寶電商分析近8年“雙十一”期間的宣傳費(fèi)用![]() (單位:萬(wàn)元)和利潤(rùn)
(單位:萬(wàn)元)和利潤(rùn)![]() (單位:十萬(wàn)元)之間的關(guān)系,得到下列數(shù)據(jù):
(單位:十萬(wàn)元)之間的關(guān)系,得到下列數(shù)據(jù):
| 2 | 3 | 4 | 5 | 6 | 8 | 9 | 11 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
(1)請(qǐng)用相關(guān)系數(shù)![]() 說(shuō)明
說(shuō)明![]() 與
與![]() 之間是否存在線性相關(guān)關(guān)系(當(dāng)
之間是否存在線性相關(guān)關(guān)系(當(dāng)![]() 時(shí),說(shuō)明
時(shí),說(shuō)明![]() 與
與![]() 之間具有線性相關(guān)關(guān)系);
之間具有線性相關(guān)關(guān)系);
(2)根據(jù)(1)的判斷結(jié)果,建立![]() 與
與![]() 之間的回歸方程,并預(yù)測(cè)當(dāng)
之間的回歸方程,并預(yù)測(cè)當(dāng)![]() 時(shí),對(duì)應(yīng)的利潤(rùn)
時(shí),對(duì)應(yīng)的利潤(rùn)![]() 為多少(
為多少(![]() 精確到0.1).
精確到0.1).
附參考公式:回歸方程中![]() 中
中![]() 和
和![]() 最小二乘估計(jì)分別為
最小二乘估計(jì)分別為
 ,相關(guān)系數(shù)
,相關(guān)系數(shù)
參考數(shù)據(jù):
 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示,在三棱柱ABC-A1B1C1中,△ABC與△A1B1C1都為正三角形且AA1⊥面ABC,F、F1分別是AC,A1C1的中點(diǎn).

求證:(1)平面AB1F1∥平面C1BF;
(2)平面AB1F1⊥平面ACC1A1.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)利用絕對(duì)值及分段函數(shù)知識(shí),將函數(shù)![]() 的解析式寫成分段函數(shù);
的解析式寫成分段函數(shù);
(2)在給出的坐標(biāo)系中畫出![]() 的圖象,并根據(jù)圖象寫出函數(shù)
的圖象,并根據(jù)圖象寫出函數(shù)![]() 的單調(diào)區(qū)間和值域.
的單調(diào)區(qū)間和值域.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在平面直角坐標(biāo)系xOy中,曲線C1: ![]() ,曲線C2:
,曲線C2: ![]() (θ為參數(shù)),以坐標(biāo)原點(diǎn)O為極點(diǎn),x軸正半軸為極軸,建立極坐標(biāo)系. (Ⅰ)求曲線C1 , C2的極坐標(biāo)方程;
(θ為參數(shù)),以坐標(biāo)原點(diǎn)O為極點(diǎn),x軸正半軸為極軸,建立極坐標(biāo)系. (Ⅰ)求曲線C1 , C2的極坐標(biāo)方程;
(Ⅱ)曲線C3: ![]() (t為參數(shù),t>0,
(t為參數(shù),t>0, ![]() )分別交C1 , C2于A,B兩點(diǎn),當(dāng)α取何值時(shí),
)分別交C1 , C2于A,B兩點(diǎn),當(dāng)α取何值時(shí), ![]() 取得最大值.
取得最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知圓![]() ,直線過點(diǎn)
,直線過點(diǎn)![]() ,且
,且![]() ,線段
,線段![]() 交圓
交圓![]() 的交點(diǎn)為點(diǎn)
的交點(diǎn)為點(diǎn)![]() ,
,![]() 是
是![]() 關(guān)于軸的對(duì)稱點(diǎn).
關(guān)于軸的對(duì)稱點(diǎn).
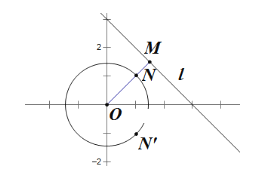
(1)求直線![]() 的方程;
的方程;
(2)已知![]() 是圓
是圓![]() 上不同的兩點(diǎn),且
上不同的兩點(diǎn),且![]() ,試證明直線
,試證明直線![]() 的斜率為定值,并求出該定值.
的斜率為定值,并求出該定值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為 ,其中
,其中![]() 為參數(shù),在以坐標(biāo)原點(diǎn)
為參數(shù),在以坐標(biāo)原點(diǎn)![]() 為極點(diǎn),
為極點(diǎn), ![]() 軸的正半軸為極軸的極坐標(biāo)系中,點(diǎn)
軸的正半軸為極軸的極坐標(biāo)系中,點(diǎn)![]() 的極坐標(biāo)為
的極坐標(biāo)為![]() , 直線
, 直線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求直線![]() 的直角坐標(biāo)方程與曲線
的直角坐標(biāo)方程與曲線![]() 的普通方程;
的普通方程;
(2)若![]() 是曲線
是曲線![]() 上的動(dòng)點(diǎn),
上的動(dòng)點(diǎn), ![]() 為線段
為線段![]() 的中點(diǎn).求點(diǎn)
的中點(diǎn).求點(diǎn)![]() 到直線
到直線![]() 的距離的最大值.
的距離的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】近年來(lái),中美貿(mào)易摩擦不斷.特別是美國(guó)對(duì)我國(guó)華為的限制.盡管美國(guó)對(duì)華為極力封鎖,百般刁難,并不斷加大對(duì)各國(guó)的施壓,拉攏他們抵制華為5G,然而這并沒有讓華為卻步.華為在2018年不僅凈利潤(rùn)創(chuàng)下記錄,海外增長(zhǎng)同樣強(qiáng)勁.今年,我國(guó)華為某一企業(yè)為了進(jìn)一步增加市場(chǎng)競(jìng)爭(zhēng)力,計(jì)劃在2020年利用新技術(shù)生產(chǎn)某款新手機(jī).通過市場(chǎng)分析,生產(chǎn)此款手機(jī)全年需投入固定成本250萬(wàn),每生產(chǎn)![]() (千部)手機(jī),需另投入成本
(千部)手機(jī),需另投入成本![]() 萬(wàn)元,且
萬(wàn)元,且  ,由市場(chǎng)調(diào)研知,每部手機(jī)售價(jià)0.7萬(wàn)元,且全年內(nèi)生產(chǎn)的手機(jī)當(dāng)年能全部銷售完.
,由市場(chǎng)調(diào)研知,每部手機(jī)售價(jià)0.7萬(wàn)元,且全年內(nèi)生產(chǎn)的手機(jī)當(dāng)年能全部銷售完.
(![]() )求出2020年的利潤(rùn)
)求出2020年的利潤(rùn)![]() (萬(wàn)元)關(guān)于年產(chǎn)量
(萬(wàn)元)關(guān)于年產(chǎn)量![]() (千部)的函數(shù)關(guān)系式,(利潤(rùn)=銷售額—成本);
(千部)的函數(shù)關(guān)系式,(利潤(rùn)=銷售額—成本);
![]() 2020年產(chǎn)量為多少(千部)時(shí),企業(yè)所獲利潤(rùn)最大?最大利潤(rùn)是多少?
2020年產(chǎn)量為多少(千部)時(shí),企業(yè)所獲利潤(rùn)最大?最大利潤(rùn)是多少?
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com