
【題目】設偶函數f(x)(x∈R)的導函數是函數f′(x),f(2)=0,當x<0時,xf′(x)﹣f(x)>0,則使得f(x)>0成立的x的取值范圍是( )
A.(﹣∞,﹣2)∪(0,2)
B.(﹣∞,﹣2)∪(2,+∞)
C.(﹣2,0)∪(2,+∞)
D.(0,2)∪(﹣2,0)
【答案】B
【解析】解:令g(x)= ![]() ,
,
∴g′(x)= ![]() ,
,
∵x<0時,xf′(x)﹣f(x)>0,
∴x<0時,g′(x)>0,
∴g(x)在(﹣∞,0)上是增函數,
∵f(x)是偶函數,∴f(﹣x)=f(x),
∴g(﹣x)= ![]() =﹣
=﹣ ![]() =﹣g(x),
=﹣g(x),
∴g(x)是奇函數,
∴g(x)在(0,+∞)上是增函數,
∵f(2)=0,∴g(2)= ![]() =0,
=0,
∴g(﹣2)=﹣g(2)=0,
如圖示: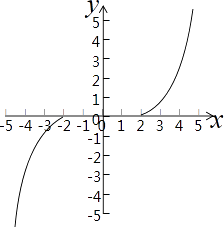
當x>0,f(x)>0,
即g(x)>0=g(2),解得:x>2,
當x<0時,f(x)<0,
即g(x)<g(﹣2)=0,解得:x<﹣2
故不等式f(x)<0的解集是(﹣∞,﹣2)∪(2,+∞),
故選:B.
構造函數g(x)= ![]() ,利用導數得到,g(x)在(﹣∞,0)是增函數,再根據f(x)為偶函數,得到g(x)是奇函數,在(0,+∞)遞增,從而求出f(x)>0的解集即可.
,利用導數得到,g(x)在(﹣∞,0)是增函數,再根據f(x)為偶函數,得到g(x)是奇函數,在(0,+∞)遞增,從而求出f(x)>0的解集即可.


科目:高中數學 來源: 題型:
【題目】如圖,直三棱柱ABC﹣A1B1C1中,AB=AC=2,AA1=3,D為BC中點, 
(1)證明:A1C∥平面B1AD;
(2)求二面角B1﹣AD﹣B的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() =1(a>b>0)的焦距為2,且過點P(1,
=1(a>b>0)的焦距為2,且過點P(1, ![]() )
)
(1)橢圓C的方程;
(2)設橢圓C的左右焦點分別為F1 , F2 , 過點F2的直線l與橢圓C交于M,N兩點.
①當直線l的傾斜角為45°時,求|MN|的長;
②求△MF1N的內切圓的面積的最大值,并求出當△MF1N的內切圓的面積取最大值時直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C過點A(1,2)和B(1,10),且與直線x﹣2y﹣1=0相切.
(1)求圓C的方程;
(2)設P為圓C上的任意一點,定點Q(﹣3,﹣6),當點P在圓C上運動時,求線段PQ中點M的軌跡方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數y=f(x)的定義域是[0,2],則函數g(x)= ![]() 的定義域是( )
的定義域是( )
A.[0,1]
B.[0,1)
C.[0,1)∪(1,4]
D.(0,1)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD是直角梯形,AD⊥AB,AB∥DC,PA⊥底面ABCD,點E為棱PC的中點.AD=DC=AP=2AB=2. 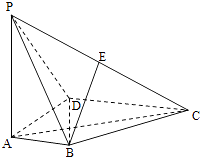
(1)證明:BE⊥平面PDC;
(2)若F為棱PC上一點,滿足BF⊥AC,求二面角F﹣AD﹣C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】連江一中第49屆田徑運動會提出了“我運動、我陽光、我健康、我快樂”的口號,某同學要設計一張如圖所示的豎向張貼的長方形海報進行宣傳,要求版心面積為162dm2(版心是指圖中的長方形陰影部分,dm為長度單位分米),上、下兩邊各空2dm,左、右兩邊各空1dm. 
(1)若設版心的高為xdm,求海報四周空白面積關于x的函數S(x)的解析式;
(2)要使海報四周空白面積最小,版心的高和寬該如何設計?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,設角A,B,C的對邊分別為a,b,c,向量 ![]() =(cosA,sinA),
=(cosA,sinA), ![]() =(
=( ![]() ﹣sinA,cosA),若
﹣sinA,cosA),若 ![]()
![]() =1.
=1.
(1)求角A的大小;
(2)若b=4 ![]() ,且c=
,且c= ![]() a,求△ABC的面積.
a,求△ABC的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com