
【題目】角![]() 是△
是△![]() 的兩個內角.下列六個條件中,“
的兩個內角.下列六個條件中,“![]() ”的充分必要條件的個數是 ( )
”的充分必要條件的個數是 ( )
①![]() ; ②
; ②![]() ; ③
; ③![]() ;
;
④![]() ; ⑤
; ⑤![]() ; ⑥
; ⑥![]() .
.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
根據大角對大邊得出A>Ba>b,結合正弦定理得出sinA>sinB>0,于是得出sin2A>sin2B,
cos2A<cos2B,然后將各條件圍繞“sinA>sinB>0,sin2A>sin2B,cos2A<cos2B”進行轉化,
即可得出答案.
當A>B時,根據“大邊對大角”可知,a>b,由于![]() ,
,
所以,sinA>sinB,則①是“A>B”的充分必要條件;
由于0<B<A<π,余弦函數y=cosx在區間(0,π)上單調遞減,
所以,cosA<cosB,則②是“A>B”的充分必要條件;
當A>B時,若A是鈍角,B為銳角,則tanA<0<tanB,則③不是“A>B”的充分必要條件;
由于0<B<A<π,則sinA>0,sinB>0,若sin2A>sin2B,則sinA>sinB,
所以,④是“A>B”的充分必要條件;
當cos2A<cos2B,即1﹣sin2A<1﹣sin2B,所以,sin2A>sin2B,
所以,⑤是“A>B”的充分必要條件;
由于tan2A>tan2B,即![]() ,即
,即![]() ,
,
所以,![]() ,則cos2A<cos2B,所以,⑥是“A>B”的充分必要條件;
,則cos2A<cos2B,所以,⑥是“A>B”的充分必要條件;
故答案為:C


 發散思維新課堂系列答案
發散思維新課堂系列答案科目:高中數學 來源: 題型:
【題目】對于任意![]() ,若數列
,若數列![]() 滿足
滿足![]() ,則稱這個數列為“K數列”.
,則稱這個數列為“K數列”.
(1)已知數列:![]() ,
,![]() ,
,![]() 是“K數列”,求實數
是“K數列”,求實數![]() 的取值范圍;
的取值范圍;
(2)設等差數列![]() 的前
的前![]() 項和為
項和為![]() ,當首項
,當首項![]() 與公差
與公差![]() 滿足什么條件時,數列
滿足什么條件時,數列![]() 是“K數列”?
是“K數列”?
(3)設數列![]() 的前
的前![]() 項和為
項和為![]() ,
,![]() ,且
,且![]() ,
,![]() . 設
. 設![]() ,是否存在實數
,是否存在實數![]() ,使得數列
,使得數列![]() 為“K數列”. 若存在,求實數
為“K數列”. 若存在,求實數![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的前
的前![]() 項和為
項和為![]() ,對一切正整數
,對一切正整數![]() ,點
,點![]() 都在函數
都在函數![]() 的圖象上,記
的圖象上,記![]() 與
與![]() 的等差中項為
的等差中項為![]() .
.
(Ⅰ)求數列![]() 的通項公式;
的通項公式;
(Ⅱ)若![]() ,求數列
,求數列![]() 的前
的前![]() 項和
項和![]() ;
;
(Ⅲ)設集合![]() ,
,![]() ,等差數列
,等差數列![]() 的任意一項
的任意一項![]() ,其中
,其中![]() 是
是![]() 中的最小數,且
中的最小數,且![]() ,求
,求![]() 的通項公式.
的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別是
的左、右焦點分別是![]() ,且離心率為
,且離心率為![]() ,點
,點![]() 為橢圓上的動點,
為橢圓上的動點,![]() 面積最大值為
面積最大值為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)![]() 是橢圓
是橢圓![]() 上的動點,且直線
上的動點,且直線![]() 經過定點
經過定點![]() ,問在
,問在![]() 軸上是否存在定點
軸上是否存在定點![]() ,使得
,使得![]() 若存在,請求出定點
若存在,請求出定點![]() ,若不存在,請說明理由.
,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD是菱形,且∠DAB=60°.點E是棱PC的中點,平面ABE與棱PD交于點F.
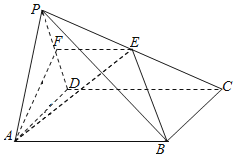
(1)求證:AB∥EF;
(2)若PA=PD=AD,且平面PAD⊥平面ABCD,求平面PAF與平面AFE所成的銳二面角的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com