
���}Ŀ����֪�E�A![]() �����ҽ��c(di��n)�քe��
�����ҽ��c(di��n)�քe��![]() �����x���ʞ�
�����x���ʞ�![]() ���c(di��n)
���c(di��n)![]() ��E�A�ϵĄ�(d��ng)�c(di��n)��
��E�A�ϵĄ�(d��ng)�c(di��n)��![]() ��e���ֵ��
��e���ֵ��![]() .
.
��1����E�A![]() �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2��![]() �ǙE�A
�ǙE�A![]() �ϵĄ�(d��ng)�c(di��n)����ֱ��
�ϵĄ�(d��ng)�c(di��n)����ֱ��![]() ��(j��ng)�^���c(di��n)
��(j��ng)�^���c(di��n)![]() ������
������![]() �S���Ƿ���ڶ��c(di��n)
�S���Ƿ���ڶ��c(di��n)![]() ��ʹ��
��ʹ��![]() �����ڣ�Ո(q��ng)������c(di��n)
�����ڣ�Ո(q��ng)������c(di��n)![]() ���������ڣ�Ո(q��ng)�f������.
���������ڣ�Ո(q��ng)�f������.
���𰸡���1��![]() ����2�����ڣ�
����2�����ڣ�![]() .
.
��������
��1�����x���ʞ�![]() ��
��![]() ��e�����
��e�����![]() ��ֵ���Ķ�����E�A�Ę�(bi��o)��(zh��n)���̣�
��ֵ���Ķ�����E�A�Ę�(bi��o)��(zh��n)���̣�
��2�����O(sh��)���ڝM���}��Ķ��c(di��n)![]() ���O(sh��)
���O(sh��)![]() ����?y��n)?/span>
����?y��n)?/span>![]() ���tֱ��
���tֱ��![]() �c
�c![]() б�ʺ͞��㣬������
б�ʺ͞��㣬������![]() ��ͨ�^����(ji��n)���Եó�
��ͨ�^����(ji��n)���Եó�![]() �c
�c![]() ���P(gu��n)ϵ���Ķ��Д��Ƿ���ڶ��c(di��n).
���P(gu��n)ϵ���Ķ��Д��Ƿ���ڶ��c(di��n).
��1��![]() ��e���ֵ�飺
��e���ֵ�飺![]() ����
����![]() ��
��![]() ����ã�
����ã�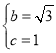 .����
.����![]() �����Է��̞飺
�����Է��̞飺![]() .
.
��2�����O(sh��)���ڝM���}��Ķ��c(di��n)![]() ���O(sh��)
���O(sh��)![]() ��
��
�O(sh��)ֱ��![]() �ķ��̞飬
�ķ��̞飬![]() .
.
��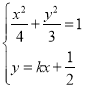 ��ȥ
��ȥ![]() ����
����![]() .
.
��ֱ��![]() �^�E�A��(n��i)һ�c(di��n)
�^�E�A��(n��i)һ�c(di��n)![]() ����
����![]() �������
�������
�������ʽ�ã�![]() ��
��
��![]() ���ɵ�ֱ��
���ɵ�ֱ��![]() �c
�c![]() б�ʺ͞���.��
б�ʺ͞���.��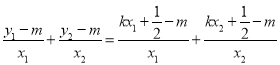 ��
��
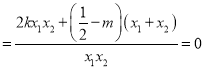 ��
��
![]()
![]() .����
.����![]() ��
��
���ڶ��c(di��n)![]() ����(d��ng)б�ʲ����ڕr(sh��)���c(di��n)
����(d��ng)б�ʲ����ڕr(sh��)���c(di��n)![]() Ҳ�����}��.
Ҳ�����}��.


 ��x��܇ϵ�д�
��x��܇ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D��ʾ����֪�����F![]() �У�����
�У�����![]() �ǵ�߅�����Σ���
�ǵ�߅�����Σ���![]() ��
��![]() �քe��
�քe��![]() �����c(di��n).
�����c(di��n).

��1���C����![]() ƽ��
ƽ��![]() ��
��
��2����![]() ��������
��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ������(ji��)�^�ס��ҡ�������Մ?w��)������P(gu��n)![]() ���Ӱ
���Ӱ![]() ��
��![]() ��
��![]() ����r.
����r.
���f���қ]�п��^�Ӱ![]() ��������
��������![]() ���Ӱ�҂�?n��i)���(g��)�����^��
���Ӱ�҂�?n��i)���(g��)�����^��
���f�������Ӱ����![]() ���Ӱ�҂�?n��i)�����ֻ��һ�˿��^��
���Ӱ�҂�?n��i)�����ֻ��һ�˿��^��
���f���Һͼ����Ӱ��![]() ����ͬ����
����ͬ����![]() ����ͬ.
����ͬ.
�����������f������Ԓ���t�ɴ˿��Д������Ӱ���ҿ��^�IJ���(sh��)�ǣ� ��
A.![]() ��B.
��B.![]() ��C.
��C.![]() ��D.
��D.![]() ����
����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�������ε�����(g��)��c(di��n)������(bi��o)�քe��![]() ��
��![]() ��
��![]() ���tԓ�����ε����ģ���߅�о����c(di��n)��������(bi��o)��
���tԓ�����ε����ģ���߅�о����c(di��n)��������(bi��o)��![]() .��@��(g��)�Y(ji��)Փ���B�������w��һ��(g��)��c(di��n)���䌦(du��)�����������ĵľ��ηQ�������w���о��������w���ėl�о�����һ�c(di��n)��ԓ�c(di��n)�Q�������w������.�������w���Ă�(g��)��c(di��n)�Ŀ��g����(bi��o)�քe��
.��@��(g��)�Y(ji��)Փ���B�������w��һ��(g��)��c(di��n)���䌦(du��)�����������ĵľ��ηQ�������w���о��������w���ėl�о�����һ�c(di��n)��ԓ�c(di��n)�Q�������w������.�������w���Ă�(g��)��c(di��n)�Ŀ��g����(bi��o)�քe��![]() ��
��![]() ��
��![]() ��
��![]() ���tԓ�����w�����ĵ�����(bi��o)�飨 ��
���tԓ�����w�����ĵ�����(bi��o)�飨 ��
A. ![]()
B. ![]()
C. ![]()
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����![]() ����
����![]() �ăɂ�(g��)��(n��i)��.��������(g��)�l���У���
�ăɂ�(g��)��(n��i)��.��������(g��)�l���У���![]() ���ij�ֱ�Ҫ�l���Ă�(g��)��(sh��)�� ( )
���ij�ֱ�Ҫ�l���Ă�(g��)��(sh��)�� ( )
��![]() �� ��
�� ��![]() �� ��
�� ��![]() ��
��
��![]() �� ��
�� ��![]() �� ��
�� ��![]() .
.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() �ĈD���^�c(di��n)
�ĈD���^�c(di��n)![]() ������
������![]() ̎ȡ�ØOֵ.
̎ȡ�ØOֵ.
��1����(du��)����![]() ��
��![]() �����,��(sh��)��(sh��)
�����,��(sh��)��(sh��)![]() ��ȡֵ����;
��ȡֵ����;
��2����(d��ng)![]() ,ԇӑՓ����(sh��)
,ԇӑՓ����(sh��)![]() �����c(di��n)��(g��)��(sh��).
�����c(di��n)��(g��)��(sh��).
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���ķքe����1,2,3,4��4����Ƭ���S�C(j��)��ȡ1�����Żغ����S�C(j��)��ȡ1�����t��õĵ�һ����Ƭ�ϵĔ�(sh��)���ڵڶ�����Ƭ�ϵĔ�(sh��)�ĸ��ʞ飨 ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���O(sh��)�溯��(sh��)f (x )�Ķ��x��?y��n)?/span>R , ��![]() , ��(d��ng)x
, ��(d��ng)x![]() �r(sh��)f (x)��
�r(sh��)f (x)��![]() , �tf (x )�څ^(q��)�g
, �tf (x )�څ^(q��)�g![]() �ϵı��_(d��)ʽ��
�ϵı��_(d��)ʽ��
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���敜����Ԫǰ5��6���o(j��)�����҇�(gu��)�R���r(sh��)���Ĕ�(sh��)�W(xu��)�ң�����_֮�ă��ӣ��������һ�lԭԭ���������(sh��)��ͬ���t�e���ݮ�.���@��ġ��硱ָˮƽ�������e������(sh��)��ָ�ߡ��@��Ԓ����˼�ǣ��ɂ�(g��)�ȸߵĎ��w�������еȸ�̎��ˮƽ�������e��ȣ��t�@�ɂ�(g��)���w�w�e��ȡ��O(sh��)�əE�A![]() �����ɵ�ƽ��D���@
�����ɵ�ƽ��D���@![]() �S���D(zhu��n)һ�ܺ�һ�ϙ��Ď��w���Q��E���w�����n���н�B�ˑ�(y��ng)���敜ԭ�������w�w�e��ʽ��������Ո(q��ng)ȴ˷�������E���w�w�e�����w�e���ڣ� ��
�S���D(zhu��n)һ�ܺ�һ�ϙ��Ď��w���Q��E���w�����n���н�B�ˑ�(y��ng)���敜ԭ�������w�w�e��ʽ��������Ո(q��ng)ȴ˷�������E���w�w�e�����w�e���ڣ� ��
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com