
【題目】已知函數![]() .
.
(1)討論函數![]() 在
在![]() 上的單調性;
上的單調性;
(2)若![]() ,當
,當![]() 時,
時,![]() ,且
,且![]() 有唯一零點,證明:
有唯一零點,證明:![]() .
.
【答案】(1)見解析;(2)證明見解析
【解析】
(1)求導后得![]() ,再對
,再對![]() 分四種情況討論可得函數的單調性;
分四種情況討論可得函數的單調性;
(2)令![]() =0,可知
=0,可知![]() 在
在![]() 上有唯一零點
上有唯一零點![]() ,所以
,所以![]() ①, 要使
①, 要使![]() 在
在![]() 上恒成立,且
上恒成立,且![]() 有唯一解,只需
有唯一解,只需![]() ,即
,即![]() ②,再聯立①②可知,
②,再聯立①②可知,![]() ,然后構造函數,利用導數可得.
,然后構造函數,利用導數可得.
(1)依題意,![]()
若![]() ,則
,則![]() ,
,
故函數![]() 在
在![]() 上單調遞增;
上單調遞增;
若![]() ,令
,令![]() ,解得
,解得![]() ;
;
若![]() ,則
,則![]() ,則
,則![]() ,
,
函數![]() 在
在![]() 上單調遞增;
上單調遞增;
若![]() ,則
,則![]() ,則
,則![]() ,
,
則函數![]() 在
在![]() 上單調遞減;
上單調遞減;
若![]() ,則
,則![]() ,則函數
,則函數![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減;
上單調遞減;
綜上所述,![]() 時,函數
時,函數![]() 在
在![]() 上單調遞增,
上單調遞增,
![]() 時,函數
時,函數![]() 在
在![]() 上單調遞減,
上單調遞減,
![]() 時,函數
時,函數![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減;
上單調遞減;
(2)依題意,![]() ,而
,而![]() ,
,
令![]() ,解得
,解得![]() ,
,
因為![]() ,故
,故![]() ,
,
故![]() 在
在![]() 上有唯一零點
上有唯一零點![]() ;
;
又![]() ,
,
故![]() ①,
①,
要使![]() 在
在![]() 上恒成立,且
上恒成立,且![]() 有唯一解,
有唯一解,
只需![]() ,即
,即![]() ②,
②,
由①②可知,![]()
令![]()
顯然![]() 在
在![]() 上單調遞減,
上單調遞減,
因為![]() ,
,
故![]() ,
,
又![]() 在
在![]() 上單調遞增,
上單調遞增,
故必有![]()


科目:高中數學 來源: 題型:
【題目】已知不等式![]() .
.
(1)是否存在實數m,使不等式對任意![]() 恒成立?并說明理由.
恒成立?并說明理由.
(2)若不等式對任意![]() 恒成立,求實數m的取值范圍.
恒成立,求實數m的取值范圍.
(3)若對于![]() ,不等式恒成立,求實數x的取值范圍.
,不等式恒成立,求實數x的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱![]() 中,底面為邊長為
中,底面為邊長為![]() 的正三角形,
的正三角形,![]() 在底面的射影為
在底面的射影為![]() 中點且
中點且![]() 到底面的距離為
到底面的距離為![]() ,已知
,已知![]() 分別是線段
分別是線段![]() 與
與![]() 上的動點,記線段
上的動點,記線段![]() 中點
中點![]() 的軌跡為
的軌跡為![]() ,則
,則![]() 等于( )(注:
等于( )(注:![]() 表示
表示![]() 的測度,本題中
的測度,本題中![]() 若分別為曲線、平面圖形、空間幾何體,分別對應為其長度、面積、體積)
若分別為曲線、平面圖形、空間幾何體,分別對應為其長度、面積、體積)
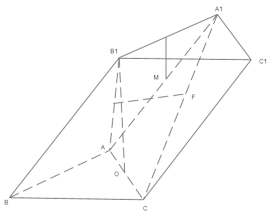
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數![]() 的定義域為D,若存在閉區間
的定義域為D,若存在閉區間![]() ,使得函數
,使得函數![]() 滿足以下兩個條件:(1)
滿足以下兩個條件:(1)![]() 在[m,n]上是單調函數;(2)
在[m,n]上是單調函數;(2)![]() 在[m,n]上的值域為[2m,2n],則稱區間[m,n]為
在[m,n]上的值域為[2m,2n],則稱區間[m,n]為![]() 的“倍值區間”.下列函數中存在“倍值區間”的有( )個.
的“倍值區間”.下列函數中存在“倍值區間”的有( )個.
①![]() ②
②![]() ③
③![]()
A.0B.1C.2D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在銳角△ABC中,∠BAC≠60°,過點B、C分別作△ABC外接圓的切線BD、CE,且滿足![]() ,直線DE與AB、AC的延長線分別交于點F、G、CF與BD交于點M,CE與BG交于點N.證明:
,直線DE與AB、AC的延長線分別交于點F、G、CF與BD交于點M,CE與BG交于點N.證明:![]() .
.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年1月8日,中共中央國務院隆重舉行國家科學技術獎勵大會,在科技界引發熱烈反響,自主創新正成為引領經濟社會發展的強勁動力.某科研單位在研發新產品的過程中發現了一種新材料,由大數據測得該產品的性能指標值y與這種新材料的含量x(單位:克)的關系為:當![]() 時,y是x的二次函數;當
時,y是x的二次函數;當![]() 時,
時,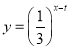 測得數據如下表(部分):
測得數據如下表(部分):
x(單位:克) | 0 | 1 | 2 | 9 | … |
y | 0 |
| 3 |
| … |
(1)求y關于x的函數關系式![]() ;
;
(2)當該產品中的新材料含量x為何值時,產品的性能指標值最大.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() (e為自然對數的底數,e=2.71828……),函數
(e為自然對數的底數,e=2.71828……),函數![]() 圖象關于直線
圖象關于直線![]() 對稱,函數
對稱,函數![]() 的最小值為m.
的最小值為m.
(I)求曲線![]() 的切線方程;
的切線方程;
(Ⅱ)求證:![]() ;
;
(III)求函數![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐P-ABC中,AC=BC=PC=2,AB=PA=PB=2![]() .
.
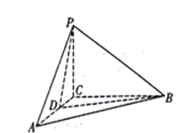
(1)證明:PC⊥平面ABC;
(2)若點D在棱AC上,且二面角D-PB-C為30°,求PD與平面PAB所成角的正弦值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com