
科目: 來源: 題型:
【題目】已知定點![]() ,
,![]() ,直線
,直線![]() 、
、![]() 相交于點
相交于點![]() ,且它們的斜率之積為
,且它們的斜率之積為![]() ,記動點
,記動點![]() 的軌跡為曲線
的軌跡為曲線![]() 。
。
(1)求曲線![]() 的方程;
的方程;
(2)過點![]() 的直線與曲線
的直線與曲線![]() 交于
交于![]() 、
、![]() 兩點,是否存在定點
兩點,是否存在定點![]() ,使得直線
,使得直線![]() 與
與![]() 斜率之積為定值,若存在,求出
斜率之積為定值,若存在,求出![]() 坐標;若不存在,請說明理由。
坐標;若不存在,請說明理由。
查看答案和解析>>
科目: 來源: 題型:
【題目】某種大型醫(yī)療檢查機器生產(chǎn)商,對一次性購買2臺機器的客戶,推出兩種超過質(zhì)保期后兩年內(nèi)的延保維修優(yōu)惠方案:方案一:交納延保金7000元,在延保的兩年內(nèi)可免費維修2次,超過2次每次收取維修費2000元;方案二:交納延保金10000元,在延保的兩年內(nèi)可免費維修4次,超過4次每次收取維修費1000元.某醫(yī)院準備一次性購買2臺這種機器。現(xiàn)需決策在購買機器時應購買哪種延保方案,為此搜集并整理了50臺這種機器超過質(zhì)保期后延保兩年內(nèi)維修的次數(shù),得下表:
維修次數(shù) | 0 | 1 | 2 | 3 |
臺數(shù) | 5 | 10 | 20 | 15 |
以這50臺機器維修次數(shù)的頻率代替1臺機器維修次數(shù)發(fā)生的概率,記X表示這2臺機器超過質(zhì)保期后延保的兩年內(nèi)共需維修的次數(shù)。
(1)求X的分布列;
(2)以所需延保金及維修費用的期望值為決策依據(jù),醫(yī)院選擇哪種延保方案更合算?
查看答案和解析>>
科目: 來源: 題型:
【題目】關于圓周率![]() ,數(shù)學發(fā)展史上出現(xiàn)過許多有創(chuàng)意的求法,如著名的普豐實驗和查理斯實驗.受其啟發(fā),我們也可以通過設計下面的實驗來估計
,數(shù)學發(fā)展史上出現(xiàn)過許多有創(chuàng)意的求法,如著名的普豐實驗和查理斯實驗.受其啟發(fā),我們也可以通過設計下面的實驗來估計![]() 的值:先請120名同學每人隨機寫下一個x,y都小于1的正實數(shù)對
的值:先請120名同學每人隨機寫下一個x,y都小于1的正實數(shù)對![]() ,再統(tǒng)計其中x,y能與1構成鈍角三角形三邊的數(shù)對
,再統(tǒng)計其中x,y能與1構成鈍角三角形三邊的數(shù)對![]() 的個數(shù)m,最后根據(jù)統(tǒng)計個數(shù)m估計
的個數(shù)m,最后根據(jù)統(tǒng)計個數(shù)m估計![]() 的值.如果統(tǒng)計結果是
的值.如果統(tǒng)計結果是![]() ,那么可以估計
,那么可以估計![]() 的值為( )
的值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 來源: 題型:
【題目】設橢圓![]()
![]() 的離心率為
的離心率為![]() ,圓
,圓![]() 與
與![]() 軸正半軸交于點
軸正半軸交于點![]() ,圓
,圓![]() 在點
在點![]() 處的切線被橢圓
處的切線被橢圓![]() 截得的弦長為
截得的弦長為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設圓![]() 上任意一點
上任意一點![]() 處的切線交橢圓
處的切線交橢圓![]() 于點
于點![]() ,
,![]() ,試判斷
,試判斷![]() 是否為定值?若為定值,求出該定值;若不是定值,請說明理由.
是否為定值?若為定值,求出該定值;若不是定值,請說明理由.
查看答案和解析>>
科目: 來源: 題型:
【題目】大學先修課程是在高中開設的具有大學水平的課程,旨在讓學有余力的高中生早接受大學思維方式、學習方法的訓練,為大學學習乃至未來的職業(yè)生涯做好準備.某高中成功開設大學先修課程已有兩年,共有![]() 人參與學習先修課程,這兩年學習先修課程的學生都參加了高校的自主招生考試(滿分
人參與學習先修課程,這兩年學習先修課程的學生都參加了高校的自主招生考試(滿分![]() 分),結果如下表所示:
分),結果如下表所示:
分數(shù) |
|
|
|
|
|
人數(shù) |
|
|
|
|
|
參加自主招生獲得通過的概率 |
|
|
|
|
|
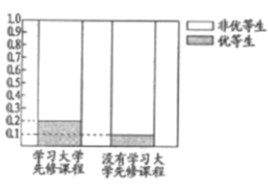
(1)這兩年學校共培養(yǎng)出優(yōu)等生![]() 人,根據(jù)圖中等高條形圖,填寫相應列聯(lián)表,并根據(jù)列聯(lián)表檢驗能否在犯錯的概率不超過
人,根據(jù)圖中等高條形圖,填寫相應列聯(lián)表,并根據(jù)列聯(lián)表檢驗能否在犯錯的概率不超過![]() 的前提下認為學習先修課程與優(yōu)等生有關系?
的前提下認為學習先修課程與優(yōu)等生有關系?
優(yōu)等生 | 非優(yōu)等生 | 總計 | |
學習大學先修課程 |
| ||
沒有學習大學先修課程 | |||
總計 |
|
(2)已知今年全校有![]() 名學生報名學習大學選項課程,并都參加了高校的自主招生考試,以前兩年參加大學先修課程學習成績的頻率作為今年參加大學先修課程學習成績的概率.
名學生報名學習大學選項課程,并都參加了高校的自主招生考試,以前兩年參加大學先修課程學習成績的頻率作為今年參加大學先修課程學習成績的概率.
(i)在今年參與大學先修課程學習的學生中任取一人,求他獲得高校自主招生通過的概率;
(ii)某班有![]() 名學生參加了大學先修課程的學習,設獲得高校自主招生通過的人數(shù)為
名學生參加了大學先修課程的學習,設獲得高校自主招生通過的人數(shù)為![]() ,求
,求![]() 的分布列和數(shù)學期望.
的分布列和數(shù)學期望.
參考數(shù)據(jù):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
參考公式: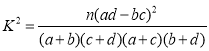 ,其中
,其中![]() .
.
查看答案和解析>>
科目: 來源: 題型:
【題目】一正方體的棱長為![]() ,作一平面
,作一平面![]() 與正方體一條體對角線垂直,且
與正方體一條體對角線垂直,且![]() 與正方體每個面都有公共點,記這樣得到的截面多邊形的周長為
與正方體每個面都有公共點,記這樣得到的截面多邊形的周長為![]() ,則( )
,則( )
A.![]() B.
B.![]() C.
C.![]() D.以上都不正確
D.以上都不正確
查看答案和解析>>
科目: 來源: 題型:
【題目】為了解某班學生喜愛打籃球是否與性別有關,對該班40名學生進行了問卷調(diào)查,得到了如下的![]() 列聯(lián)表:
列聯(lián)表:
男生 | 女生 | 總計 | |
喜愛打籃球 | 19 | 15 | 34 |
不喜愛打籃球 | 1 | 5 | 6 |
總計 | 20 | 20 | 40 |
(1)在女生的20個個體中,隨機抽取2人,記隨機變量![]() 為抽到“不喜愛籃球”的人數(shù),求
為抽到“不喜愛籃球”的人數(shù),求![]() 的分布列及數(shù)學期望
的分布列及數(shù)學期望![]() ;
;
(2)判斷能否在犯錯誤的概率不超過0.1的條件下認為喜愛籃球與性別有關?
附: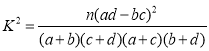 ,其中
,其中![]() .
.
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com