
四川省遂寧市2009屆高三第三次診斷性考試(數學文)
本試卷分第I卷(選擇題)和第Ⅱ卷(非選擇題)兩部分。第I卷1至3頁。第Ⅱ卷4至10頁。總分150分,考試時間120分鐘。考試結束后,將第Ⅱ卷和答題卡一并交回。
第I卷
注意事項:
1.答第I卷前,考生務必將自己的姓名、考號、學校、考試科目涂寫在答題卡上。
2.每小題選出答案后,用鉛筆把答題卡上對應題目的答案標號涂黑。如需改動,用橡皮擦干凈后,在選涂其他答案標號。不能答在試卷上。
3.本卷共12小題,每小題5分,共60分。在每小題給出的四個選項中,只有一項是符合題目要求的。
參考公式:
如果事件 、
、 互斥,那么
球的表面積公式
互斥,那么
球的表面積公式


如果事件 、
、 相互獨立,那么
其中
相互獨立,那么
其中 表示球的半徑
表示球的半徑
 球的體積公式
球的體積公式
如果事件 在一次實驗中發生的概率為
在一次實驗中發生的概率為 ,那么
,那么

 次獨立重復實驗中恰好發生
次獨立重復實驗中恰好發生 次的概率
其中
次的概率
其中 表示球的半徑
表示球的半徑

一、選擇題
1.已知全集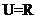 ,
,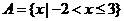 ,
,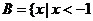 或
或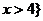 ,那么集合
,那么集合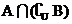
A.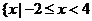 }
B.
}
B.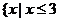 或
或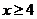 }
}
C.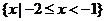 D.
D.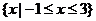

 2.函數
2.函數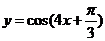 的圖象的兩條相鄰對稱軸間的距離為
的圖象的兩條相鄰對稱軸間的距離為
 A.
A.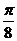 B.
B.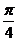 C.
C.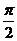 D.
D.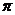
 3.在
3.在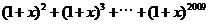 的展開式中的
的展開式中的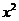 系數等于
系數等于
 A.
A.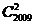 B.
B.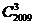 C.
C.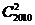 D.
D.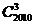
 4.直線
4.直線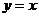 截圓
截圓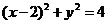 所得的弦長為
所得的弦長為
 A.1
B.
A.1
B.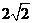 C.2
D.
C.2
D.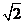
 5.平面
5.平面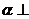 平面
平面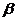 的一個充要條件是
的一個充要條件是
 A.存在一個平面
A.存在一個平面 B.存在一條直線
B.存在一條直線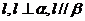
 C.存在一個平面
C.存在一個平面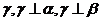 D.存在一條直線
D.存在一條直線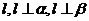
 6.若是實數
6.若是實數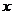 滿足
滿足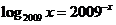 ,則下列不等關系正確的是
,則下列不等關系正確的是
 A.
A.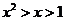 B.
B.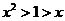 C.
C.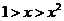 D.
D.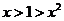
 7.在等差數列
7.在等差數列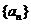 中,
中,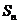 為前
為前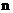 項和,且
項和,且 ,則
,則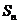 中最大的是
中最大的是
 A.
A.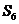 B.
B.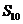 C.
C.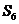 或
或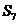 D.
D.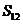
 8.如果以原點為圓心的圓必過雙曲線
8.如果以原點為圓心的圓必過雙曲線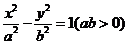 的焦點,而且被雙曲線
的焦點,而且被雙曲線
 的右準線分成2:1的兩段圓弧。那么該雙曲線的離心率為
的右準線分成2:1的兩段圓弧。那么該雙曲線的離心率為
 A.
A.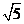 B.
B.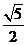 C.
C.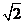 D.
D.
 9.四面體
9.四面體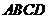 的外接球球心在
的外接球球心在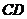 上,且
上,且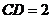 ,
,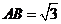 ,在外接球面上
,在外接球面上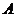 ,
,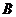
 兩點間的球面距離是
兩點間的球面距離是
 A.
A.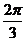 B.
B.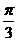 C.
C.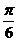 D.
D.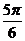



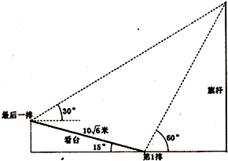 10.北京2008年第29屆奧運會開幕式上舉行升旗儀式,在坡度15°的看臺上,同一列上的第一排和最后一排測得旗桿頂部的仰角分別為60°和30°,第一排和最后一排的距離 為
10.北京2008年第29屆奧運會開幕式上舉行升旗儀式,在坡度15°的看臺上,同一列上的第一排和最后一排測得旗桿頂部的仰角分別為60°和30°,第一排和最后一排的距離 為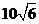 米(如圖所示),旗桿底部與第一排在一個水平面上,已知國歌長度約為50秒,升旗手勻速升旗的速度為
米(如圖所示),旗桿底部與第一排在一個水平面上,已知國歌長度約為50秒,升旗手勻速升旗的速度為
 A.
A.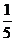 (米/秒) B.
(米/秒) B.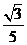 (米/秒)
(米/秒)


 C.
C.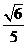 (米/秒) D.
(米/秒) D.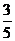 (米/秒)
(米/秒)


 11.已知正方體
11.已知正方體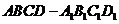 中,
中,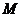 為
為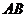 中點,棱長為2,
中點,棱長為2,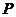 是平面
是平面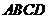 上的動點,且滿足條件
上的動點,且滿足條件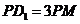 ,則動點
,則動點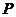 在平面
在平面 上形成的軌跡是
上形成的軌跡是
 A.圓 B.橢圓
C.雙曲線
D.拋物線
A.圓 B.橢圓
C.雙曲線
D.拋物線
 12.若自然數
12.若自然數 使得作豎式加法
使得作豎式加法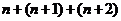 均不產生進位現象,則稱
均不產生進位現象,則稱 為“可連數”。例如:32是“可連數”,因32+33+34不產生進位現象;23不是“可連數”,因23+24+25產生進位現象,那么,小于100的“可連數”的個數為
為“可連數”。例如:32是“可連數”,因32+33+34不產生進位現象;23不是“可連數”,因23+24+25產生進位現象,那么,小于100的“可連數”的個數為
 A.9
B.
A.9
B.




 遂寧市高中2009屆第三次診斷性考試
遂寧市高中2009屆第三次診斷性考試
 數 學(文史類)
數 學(文史類)

 第Ⅱ卷
第Ⅱ卷
 注意事項:
注意事項:
 1.用鋼筆或圓珠筆直接答在試題卷中;
1.用鋼筆或圓珠筆直接答在試題卷中;
 2.答卷前將密封線內的項目填寫清楚;
2.答卷前將密封線內的項目填寫清楚;
 3.本卷共10小題,共90分。
3.本卷共10小題,共90分。
題號
二
三
總分
17
18
19
20
21
22
分數
 二、填空題:本大題共4小題,每小題4分,共16分。把答案填在題中橫線上。
二、填空題:本大題共4小題,每小題4分,共16分。把答案填在題中橫線上。
 13.已知
13.已知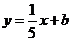 與
與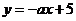 互為反函數,則
互為反函數,則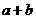 =___________________。
=___________________。
 14.已知
14.已知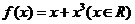 ,則不等式
,則不等式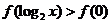 的解集為______________。
的解集為______________。
 15.已知
15.已知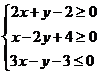 ,則
,則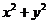 的最小值是_____________。
的最小值是_____________。

 16.下列四個命題中:
16.下列四個命題中:
 ①將函數
①將函數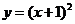 的圖象按向量
的圖象按向量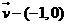 平移得到的圖象對應的函數表達式為
平移得到的圖象對應的函數表達式為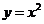 ;
;
 ②已知平面向量
②已知平面向量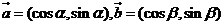 ,若
,若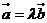 ,則實數
,則實數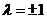 ;
;
 ③
③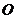 是
是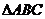 的重心,則
的重心,則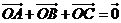
 ④
④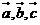 兩兩所成角相等,
兩兩所成角相等,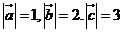 那么
那么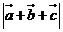 是
是
 其中是真命題的序號是________________________________________。
其中是真命題的序號是________________________________________。

 三、解答題:本大題共6個小題,共74分,解答應寫出文字說明、證明過程或演算步驟。
三、解答題:本大題共6個小題,共74分,解答應寫出文字說明、證明過程或演算步驟。
 17.(本小題滿分12分)
17.(本小題滿分12分)
 已知向量
已知向量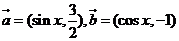
 (I)當
(I)當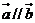 時,求
時,求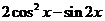 的值;
的值;
 (Ⅱ)求
(Ⅱ)求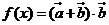 在
在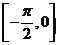 上的值域。
上的值域。




























 18.(本小題滿分12分)
18.(本小題滿分12分)

 在某社區舉辦的《2008奧運知識有獎問答比賽》中,甲、乙、丙三人同時回答一道有關奧運知識的問題,已知甲回答對這道題的概率是
在某社區舉辦的《2008奧運知識有獎問答比賽》中,甲、乙、丙三人同時回答一道有關奧運知識的問題,已知甲回答對這道題的概率是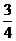 ,甲、丙兩人都回答錯的概率是
,甲、丙兩人都回答錯的概率是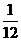 ,乙、丙兩人都回答對的概率是
,乙、丙兩人都回答對的概率是
 (I)求乙、丙兩人各自回答對這道題的概率;
(I)求乙、丙兩人各自回答對這道題的概率;
 (Ⅱ)求甲、乙、丙三人中恰有兩人回答對該題的概率。
(Ⅱ)求甲、乙、丙三人中恰有兩人回答對該題的概率。





19.(本小題滿分12分)
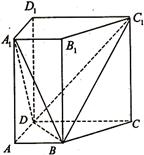 如圖所示,已知直四棱柱
如圖所示,已知直四棱柱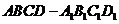 中,
中,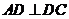 ,
,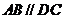 ,且滿足
,且滿足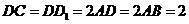
(I)求證: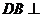 平面
平面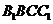 ;
;
(Ⅱ)求二面角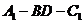 的余弦值。
的余弦值。
20.(本小題滿分12分)
已知函數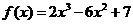
(I)求函數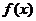 的單調區間;
的單調區間;
(Ⅱ)若關于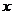 的方程
的方程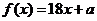 有三個相異實根,求實數
有三個相異實根,求實數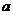 的取值范圍。
的取值范圍。
21.(本小題滿分12分)
已知數列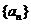 是等差數列,
是等差數列,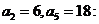 數列
數列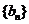 的前
的前 項和是
項和是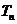 ,且
,且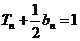
(I)求數列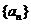 的通項公式;
的通項公式;
(Ⅱ)求證:數列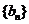 是等比數列;
是等比數列;
(Ⅲ)記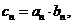 求
求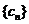 的前
的前 項和
項和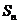 。
。
22.(本小題滿分14分)
過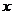 軸上動點
軸上動點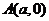 引拋物線
引拋物線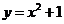 的兩條切線
的兩條切線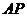 、
、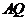 ,切點分別為
,切點分別為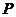 、
、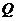
(I)若切線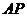 ,
,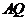 的斜率分別是
的斜率分別是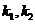 ,求證:
,求證: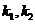 為定值;
為定值;
(Ⅱ)求證:直線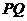 過定點,并求出定點的坐標
過定點,并求出定點的坐標
(Ⅲ)要使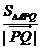 最小,求
最小,求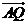 ?
?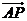 的值
的值
遂寧市高中2009屆第三次診斷性考試
一、選擇題(每小題5分,滿分60分)
1
2
3
4
5
6
7
8
9
10
11
12
D
C
D
B
B
A
C
C
A
D
A
D
二、填空題(每小題4分,滿分16分)
13.-6 14. 15.
15. 16.②③
16.②③
三、解答題(第17、18、19、20、21題各12分,第22題14分,共74分)
17.(I)

(Ⅱ)



 函數
函數 的值域為
的值域為
18.解:(I)記“甲回答對這道題”、“乙回答對這道題”、“丙回答對這道題”分別為事件
 、
、 、
、 ,則
,則 ,且有
,且有 即
即

(Ⅱ)由(1)
則甲、乙、丙三人中恰有兩人回答對該題的概率為:

19.解:法一
(I)設 是
是 的中點,連結
的中點,連結 ,
,
則四邊形 為方形,
為方形, ,故
,故 ,
,

 即
即
又
 平面
平面
(Ⅱ)由(I)知 平面
平面 ,
,
又 平面
平面 ,
, ,
,
取 的中點
的中點 ,連結
,連結 又
又 ,
,
則 ,取
,取 的中點
的中點 ,連結
,連結 則
則
 為二面角
為二面角 的平面角
的平面角
連結 ,在
,在 中,
中, ,
,
取 的中點
的中點 ,連結
,連結 ,
, ,在
,在 中,
中,

 二面角
二面角 的余弦值為
的余弦值為
法二:
 (I)以
(I)以 為原點,
為原點, 所在直線分別為
所在直線分別為 軸,
軸, 軸,
軸, 軸建立如圖所示的空間直角坐標系,則
軸建立如圖所示的空間直角坐標系,則


又因為
所以, 平面
平面
(Ⅱ)設 為平面
為平面 的一個法向量。
的一個法向量。
由 得
得
取 ,則
,則 又
又 ,
,
設 為平面
為平面 的一個法向量,由
的一個法向量,由 ,
, ,
,
得 取
取 取
取
設 與
與 的夾角為
的夾角為 ,二面角
,二面角 為
為 ,顯然
,顯然 為銳角,
為銳角,
 ,即為所求
,即為所求
20.解:(I) 或
或
故 的單調遞增區間是
的單調遞增區間是 和
和
單調遞減區間是(0,2)
(Ⅱ)



 在
在 和
和 遞增,在(-1,3)遞減。
遞增,在(-1,3)遞減。
 有三個相異實根
有三個相異實根

21.解:(I)設 的公差為
的公差為 ,則:
,則:

(Ⅱ)當 時,
時, ,由
,由 ,得
,得
當 時,
時, ,
,
 ,即
,即
 是以
是以 為首項,
為首項, 為公比的等比數列。
為公比的等比數列。
(Ⅲ)由(Ⅱ)可知:


22.解:(I)設過 與拋物線
與拋物線 的相切的直線的斜率是
的相切的直線的斜率是 ,
,
則該切線的方程為:
由 得
得

則 都是方程
都是方程 的解,故
的解,故
(Ⅱ)設
由于 ,故切線
,故切線 的方程是:
的方程是:
則
 ,同理
,同理
則直線 的方程是
的方程是 ,則直線
,則直線 過定點(0,2)
過定點(0,2)
(Ⅲ)要使 最小,就是使得
最小,就是使得 到直線
到直線 的距離最小,而
的距離最小,而 到直線
到直線 的距離
的距離

當且僅當 即
即 時取等號
時取等號
設
由 得
得 ,則
,則



湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com