
題目列表(包括答案和解析)
設橢圓![]() 的焦點分別為F1(-1,0)、F2(1,0),右準線l交x軸于點A,且
的焦點分別為F1(-1,0)、F2(1,0),右準線l交x軸于點A,且![]() .
.
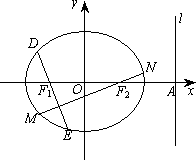
(Ⅰ)試求橢圓的方程;
(Ⅱ)過F1、F2分別作互相垂直的兩直線與橢圓分別交于D、E、M、N四點(如圖所示),試求四邊形DMEN面積的最大值和最小值
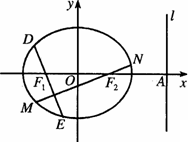
設橢圓的焦點分別為F1(-1,0)、F2(1,0),右準線l交x軸于點A,且![]() .
.
(1)求橢圓的方程;
(2)過F1、F2分別作互相垂直的兩直線與橢圓分別交于D、E、M、N四點(如圖所示),試求四邊形DMEN面積的最大值和最小值.
設點 是曲線
是曲線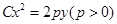 上的動點,點
上的動點,點 到點(0,1)的距離和它到焦點
到點(0,1)的距離和它到焦點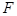 的距離之和的最小值為
的距離之和的最小值為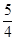 .
.
(1)求曲線C的方程;
(2)若點 的橫坐標為1,過
的橫坐標為1,過 作斜率為
作斜率為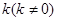 的直線交
的直線交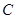 于點
于點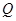 ,交
,交 軸于點
軸于點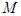 ,過點
,過點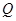 且與
且與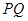 垂直的直線與
垂直的直線與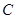 交于另一點
交于另一點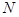 ,問是否存在實數(shù)
,問是否存在實數(shù)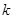 ,使得直線
,使得直線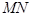 與曲線
與曲線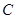 相切?若存在,求出
相切?若存在,求出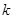 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
設點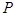 是曲線
是曲線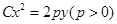 上的動點,點
上的動點,點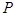 到點(0,1)的距離和它到焦點
到點(0,1)的距離和它到焦點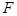 的距離之和的最小值為
的距離之和的最小值為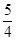 .
.
(1)求曲線C的方程;
(2)若點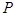 的橫坐標為1,過
的橫坐標為1,過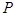 作斜率為
作斜率為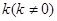 的直線交
的直線交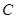 于點
于點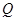 ,交
,交 軸于點
軸于點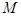 ,過點
,過點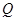 且與
且與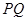 垂直的直線與
垂直的直線與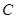 交于另一點
交于另一點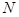 ,問是否存在實數(shù)
,問是否存在實數(shù)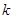 ,使得直線
,使得直線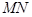 與曲線
與曲線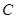 相切?若存在,求出
相切?若存在,求出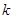 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
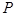 是曲線
是曲線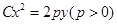 上的動點,點
上的動點,點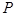 到點(0,1)的距離和它到焦點
到點(0,1)的距離和它到焦點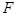 的距離之和的最小值為
的距離之和的最小值為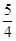 .
. 的橫坐標為1,過
的橫坐標為1,過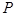 作斜率為
作斜率為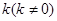 的直線交
的直線交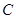 于點
于點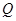 ,交
,交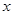 軸于點
軸于點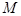 ,過點
,過點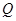 且與
且與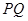 垂直的直線與
垂直的直線與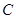 交于另一點
交于另一點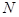 ,問是否存在實數(shù)
,問是否存在實數(shù)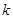 ,使得直線
,使得直線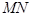 與曲線
與曲線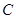 相切?若存在,求出
相切?若存在,求出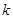 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.一、選擇題(5分×12=60分)
B B D D C B B D D C A A
二、填空題(4分x 4=16分)
13.0.1
14.63
15.學.files/image384.gif) 16.①③
16.①③
三、解答題(12分×5+14分=74分)
17.解:(1)學.files/image386.gif) 2分
2分
學.files/image388.gif) ……………………4分
……………………4分
學.files/image390.gif) ∴
∴學.files/image284.gif) 的最小正周期為
的最小正周期為學.files/image393.gif) …………………6分(2)∵
…………………6分(2)∵學.files/image395.gif) 成等比數(shù)列 ∴
成等比數(shù)列 ∴學.files/image397.gif)
∴學.files/image399.gif) ≥
≥學.files/image401.gif) ………………………8分
………………………8分
∵學.files/image403.gif) ∴
∴學.files/image158.gif)
學.files/image406.gif)
學.files/image294.gif) ≤
≤學.files/image409.gif) 即
即
學.files/image411.gif) ≤
≤學.files/image409.gif)
學.files/image414.gif)
∵學.files/image416.gif) ∴
∴學.files/image418.gif) ≤
≤學.files/image380.gif) ………………………………………………10分
………………………………………………10分
18.解:(1)設學.files/image040.gif) 公差
公差學.files/image422.gif) 由
由學.files/image424.gif) 成等比數(shù)列得
成等比數(shù)列得學.files/image426.gif) …………………1分
…………………1分
∴即學.files/image428.gif) ∴
∴學.files/image430.gif) 舍去或
舍去或學.files/image432.gif) …………………………3分
…………………………3分
∴學.files/image434.gif) ………………………………………………4分
………………………………………………4分
又學.files/image436.gif) ………………………………………………5分
………………………………………………5分
∴學.files/image438.gif)
學.files/image440.gif) ………………………………………7分
………………………………………7分
(2)學.files/image442.gif) ………………………………………………8分
………………………………………………8分
當學.files/image444.gif) 時,
時,學.files/image446.gif) ………………………………………10分
………………………………………10分
當學.files/image448.gif) 時,
時,學.files/image450.gif) …………………………7分
…………………………7分
19.解:(1)記“任取2張卡片,將卡片上的函數(shù)相加得到偶函數(shù)”為事件A,
學.files/image452.gif) ……………………………………………………4分
……………………………………………………4分
(2)學.files/image215.gif) 可能值為
可能值為學.files/image455.gif) ……………………………………………………………5分
……………………………………………………………5分
學.files/image457.gif)
學.files/image459.gif) …………………………10分
…………………………10分
∴學.files/image461.gif) …………………………12分
…………………………12分
20.解:(1)連結學.files/image463.gif)
學.files/image465.gif)
學.files/image467.gif) 為正△
…1分
為正△
…1分
學.files/image468.gif)
學.files/image469.gif)
學.files/image471.gif)
學.files/image473.gif)
學.files/image475.gif)
學.files/image475.gif)
學.files/image478.gif) 面
面學.files/image480.gif)
學.files/image482.gif) 3分
3分
面學.files/image484.gif) 面
面學.files/image486.gif)
學.files/image488.gif)
學.files/image475.gif)
學.files/image490.gif)
即點學.files/image325.gif) 的位置在線段
的位置在線段學.files/image327.gif) 的四等分點且靠近
的四等分點且靠近學.files/image494.gif) 處 ………………………………………6分(2)過
處 ………………………………………6分(2)過學.files/image163.gif) 作
作學.files/image497.gif) 于
于學.files/image116.gif) ,連
,連學.files/image500.gif)
學.files/image502.jpg) 由(1)知
由(1)知學.files/image478.gif) 面
面學.files/image505.gif) (三垂線定理)
(三垂線定理)
∴學.files/image507.gif) 為二面角
為二面角學.files/image509.gif) 的平面角……9分
的平面角……9分
學.files/image511.gif)
學.files/image513.gif)
學.files/image515.gif)
學.files/image517.gif)
在學.files/image519.gif) 中,
中,學.files/image521.gif)
在學.files/image523.gif) 中,
中,學.files/image525.gif)
∴二面角學.files/image509.gif) 的大小為
的大小為學.files/image527.gif) ………………………………………12分
………………………………………12分
(說明:若用空間向量解,請參照給分)
學.files/image529.jpg) 21.解:(1)設
21.解:(1)設學.files/image531.gif) ,由
,由學.files/image533.gif) 取
取學.files/image535.gif) 得
得
學.files/image537.gif)
學.files/image539.gif)
則學.files/image541.gif) ……………………2分
……………………2分
∴學.files/image543.gif) …………………………12分
…………………………12分
又∵學.files/image545.gif) 為定值,
為定值,學.files/image547.gif) 則
則學.files/image549.gif) ………………5分
………………5分
∵學.files/image551.gif) 為定值,∴
為定值,∴學.files/image553.gif) 為定值。
為定值。
(2)∵學.files/image360.gif) ,∴拋物線方程為:
,∴拋物線方程為:學.files/image556.gif) 設點
設點學.files/image558.gif) 則
則學.files/image560.gif)
由(1)知學.files/image562.gif) 則
則學.files/image564.gif) ………………………………8分
………………………………8分
又∵學.files/image348.gif) 過點
過點學.files/image567.gif) ∴
∴學.files/image569.gif) ∴
∴學.files/image571.gif) ∴
∴學.files/image573.gif) ………………………………9分
………………………………9分
代入橢圓學.files/image575.gif) 方程得:
方程得:學.files/image577.gif)
∴學.files/image579.gif) ≥
≥學.files/image581.gif) ………………11分
………………11分
學.files/image582.gif)
學.files/image583.gif)
學.files/image584.gif)
學.files/image586.gif)
當且僅當 即 上式取等號
學.files/image588.gif)
學.files/image590.gif)
∴此時橢圓的方程為:學.files/image592.gif) ………………………………………12分
………………………………………12分
22.解:(1)∵ 學.files/image594.gif) ∴
∴學.files/image596.gif) …1分
…1分
設學.files/image598.gif)
學.files/image600.gif) 則
則學.files/image602.gif) ……2分
……2分
∴學.files/image604.gif) 在
在學.files/image370.gif) 上為減函數(shù) 又
上為減函數(shù) 又學.files/image607.gif)
學.files/image609.gif) 時,
時,學.files/image604.gif)
學.files/image611.gif) ,∴
,∴學.files/image613.gif) ∴
∴學.files/image284.gif) 在
在學.files/image370.gif) 上是減函數(shù)………4分(2)①∵
上是減函數(shù)………4分(2)①∵學.files/image617.gif) ∴
∴學.files/image619.gif) 或
或學.files/image110.gif) 時
時
學.files/image622.gif) ∴
∴學.files/image624.gif) …………………………………6分
…………………………………6分
學.files/image158.gif) 又≤
又≤學.files/image172.gif) ≤
≤學.files/image374.gif) 對一切
對一切學.files/image376.gif) 恒成立
∴
恒成立
∴學.files/image158.gif) ≤
≤學.files/image172.gif) ≤
≤學.files/image264.gif) ……………8分
……………8分
②顯然當學.files/image633.gif) 或
或學.files/image635.gif) 時,不等式成立
…………………………9分
時,不等式成立
…………………………9分
當學.files/image637.gif) ,原不等式等價于
,原不等式等價于學.files/image639.gif) ≥
≥學.files/image641.gif) ………10分
………10分
下面證明一個更強的不等式:學.files/image639.gif) ≥
≥學.files/image643.gif) …①
…①
即學.files/image645.gif) ≥
≥學.files/image647.gif) ……②亦即
……②亦即學.files/image649.gif) ≥
≥學.files/image651.gif) …………………………11分
…………………………11分
由(1) 知學.files/image651.gif) 在
在學.files/image654.gif) 上是減函數(shù) 又
上是減函數(shù) 又學.files/image656.gif) ∴
∴學.files/image658.gif) ……12分
……12分
∴不等式②成立,從而①成立 又學.files/image660.gif)
學.files/image641.gif)
∴學.files/image639.gif) >
>學.files/image641.gif)
綜合上面∴學.files/image663.gif) ≤
≤學.files/image124.gif) ≤
≤學.files/image380.gif) 且
且學.files/image663.gif) ≤
≤學.files/image172.gif) ≤
≤學.files/image669.gif) 時,原不等式成立 ……………………………14分
時,原不等式成立 ……………………………14分
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com