
3、已知一次函數y=kx+b,當-3≤x≤1時,對應y的值為1≤y≤9.則k·b的值( )
(A)14 (B)-6
(C) -6或21 (D) -6或14
[命題意圖]考查一次函數的增減性,試題亮點是滲透了分類討論思想,許多學生沒有進行分類求解,選A或B
[參考答案]D
[試題來源]原創題
2、如圖,圓柱形開口杯底部固定在長方體水池底,向水池勻速注入水(倒在杯外),水池中水面高度是h,注水時間為t,則h與t之間的關系大致為下圖中的 ( )
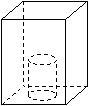
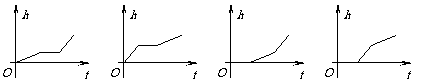
A B C D
[命題意圖]探索具體問題中的數量關系和變化規律類問題,考綱要求D級靈活運用,這類問題情境來源于生活,如龜兔賽跑,烏鴉喝水等,重視對學生學習數學知識與技能的結果和過程的評價。
[參考答案] B
[試題來源]改編題
1、下列實數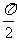 ,sin30°,0.1414,
,sin30°,0.1414,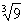 ,0.383383338…… , 22/7中,無理數的個數是
,0.383383338…… , 22/7中,無理數的個數是
A、2個 B、3個 C、4個 D、5個
[命題意圖]考查學生對無理數的認識,無理數的概念比較抽象,講評時,要求學生了解常見無理數的四種形式。
常見無理數:含有π的的式子
根號形(開方開不盡的)
構造型
三角函數形(值不是有理數)
[參考答案] B
[試題來源]原創題
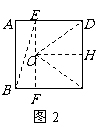
18.一種電訊信號轉發裝置的發射直徑為31km.現要求:在一邊長為30km的正方形城區選擇若干個安裝點,每個點安裝一個這種轉發裝置,使這些裝置轉發的信號能完全覆蓋這個城市.問:
(1)能否找到這樣的4個安裝點,使得這些點安裝了這種轉發裝置后能達到預設的要求?
(2)至少需要選擇多少個安裝點,才能使這些點安裝了這種轉發裝置后達到預設的要求?
 答題要求:請你在解答時,畫出必要的示意圖,并用必要的計算、推理和文字來說明你的理由.(下面給出了幾個邊長為30km的正方形城區示意圖,供解題時選用)
答題要求:請你在解答時,畫出必要的示意圖,并用必要的計算、推理和文字來說明你的理由.(下面給出了幾個邊長為30km的正方形城區示意圖,供解題時選用)
(2008年無錫,本題考查知識點很多,對提高學生審題能力,分析問題能力有很大幫助,有利于學生將自己的思維過程有條理的表達出來, 有利于學生學好數學的思維品質的培養)
答案:(1)將圖1中的正方形等分成如圖的四個小正方形,將這4個轉發裝置安裝在這4個小正方形對角線的交點處,此時,每個小正方形的對角線長為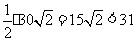 ,每個轉發裝置都能完全覆蓋一個小正方形區域,故安裝4個這種裝置可以達到預設的要求.
,每個轉發裝置都能完全覆蓋一個小正方形區域,故安裝4個這種裝置可以達到預設的要求.
(圖案設計不唯一)
(2)將原正方形分割成如圖2中的3個矩形,使得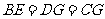 .將每個裝置安裝在這些矩形的對角線交點處,設
.將每個裝置安裝在這些矩形的對角線交點處,設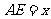 ,則
,則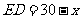 ,
,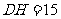 .
.
由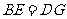 ,得
,得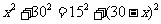 ,
,
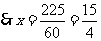 ,
,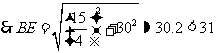 ,
,
即如此安裝3個這種轉發裝置,也能達到預設要求.
或:將原正方形分割成如圖2中的3個矩形,使得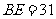 ,
, 是
是 的中點,將每個裝置安裝在這些矩形的對角線交點處,則
的中點,將每個裝置安裝在這些矩形的對角線交點處,則 ,
,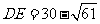 ,
, 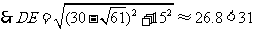 ,即如此安裝三個這個轉發裝置,能達到預設要求.
,即如此安裝三個這個轉發裝置,能達到預設要求.
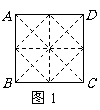
要用兩個圓覆蓋一個正方形,則一個圓至少要經過正方形相鄰兩個頂點.如圖3,用一個直徑為31的 去覆蓋邊長為30的正方形
去覆蓋邊長為30的正方形 ,設
,設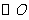 經過
經過 ,
,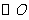 與
與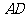 交于
交于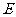 ,連
,連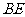 ,則
,則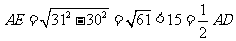 ,這說明用兩個直徑都為31的圓不能完全覆蓋正方形
,這說明用兩個直徑都為31的圓不能完全覆蓋正方形 .
.
所以,至少要安裝3個這種轉發裝置,才能達到預設要求.
評分說明:示意圖(圖1、圖2、圖3)每個圖1分.

17.某公司有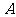 型產品40件,
型產品40件, 型產品60件,分配給下屬甲、乙兩個商店銷售,其中70件給甲店,30件給乙店,且都能賣完.兩商店銷售這兩種產品每件的利潤(元)如下表:
型產品60件,分配給下屬甲、乙兩個商店銷售,其中70件給甲店,30件給乙店,且都能賣完.兩商店銷售這兩種產品每件的利潤(元)如下表:
|
|
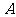 型利潤 型利潤 |
 型利潤 型利潤 |
|
甲店 |
200 |
170 |
|
乙店 |
160 |
150 |
(1)設分配給甲店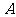 型產品
型產品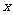 件,這家公司賣出這100件產品的總利潤為
件,這家公司賣出這100件產品的總利潤為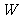 (元),求
(元),求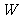 關于
關于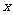 的函數關系式,并求出
的函數關系式,并求出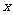 的取值范圍;
的取值范圍;
(2)若公司要求總利潤不低于17560元,說明有多少種不同分配方案,并將各種方案設計出來;
(3)為了促銷,公司決定僅對甲店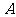 型產品讓利銷售,每件讓利
型產品讓利銷售,每件讓利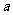 元,但讓利后
元,但讓利后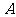 型產品的每件利潤仍高于甲店
型產品的每件利潤仍高于甲店 型產品的每件利潤.甲店的
型產品的每件利潤.甲店的 型產品以及乙店的
型產品以及乙店的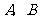 型產品的每件利潤不變,問該公司又如何設計分配方案,使總利潤達到最大?
型產品的每件利潤不變,問該公司又如何設計分配方案,使總利潤達到最大?
(2008年黃石市,考查學生運用不等式組解決實際問題的能力及解決方案問題的思維方法)
答案:依題意,甲店 型產品有
型產品有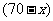 件,乙店
件,乙店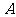 型有
型有 件,
件, 型有
型有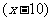 件,則
件,則
(1)
 .
.
由 解得
解得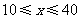 .
.
(2)由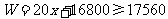 ,
,
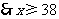 .
.
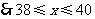 ,
,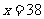 ,39,40.
,39,40.
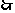 有三種不同的分配方案.
有三種不同的分配方案.
①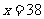 時,甲店
時,甲店 型38件,
型38件, 型32件,乙店
型32件,乙店 型2件,
型2件, 型28件.
型28件.
②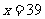 時,甲店
時,甲店 型39件,
型39件, 型31件,乙店
型31件,乙店 型1件,
型1件, 型29件.
型29件.
③ 時,甲店
時,甲店 型40件,
型40件, 型30件,乙店
型30件,乙店 型0件,
型0件, 型30件.
型30件.
(3)依題意:
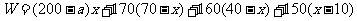
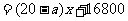 .
.
①當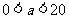 時,
時, ,即甲店
,即甲店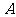 型40件,
型40件, 型30件,乙店
型30件,乙店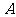 型0件,
型0件, 型30件,能使總利潤達到最大.
型30件,能使總利潤達到最大.
②當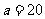 時,
時,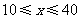 ,符合題意的各種方案,使總利潤都一樣.
,符合題意的各種方案,使總利潤都一樣.
③當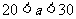 時,
時,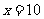 ,即甲店
,即甲店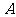 型10件,
型10件, 型60件,乙店
型60件,乙店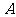 型30件,
型30件, 型0件,能使總利潤達到最大.
型0件,能使總利潤達到最大.
16.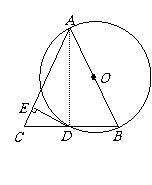 如圖,AB是⊙O的直徑,BD是⊙O的弦,延長BD到點C,使DC=BD,連結AC,過點D作DE⊥AC,垂足為E.
如圖,AB是⊙O的直徑,BD是⊙O的弦,延長BD到點C,使DC=BD,連結AC,過點D作DE⊥AC,垂足為E.
(1)求證:AB=AC;
(2)求證:DE為⊙O的切線;
(3)若⊙O的半徑為5,∠BAC=60°,求DE的長.
(2008年施恩自治州,本題知識點有圓的直徑定義、圓的切線判別、等邊三角形概念、三角函數等,考查學生分析問題綜合運用所學知識解決問題的能力)
答案:(1)證明:連接AD
∵AB是⊙O的直徑
∴∠ADB=90°
又BD=CD
∴AD是BC的垂直平分線
∴AB=AC
(2)連接OD
∵點O、D分別是AB、BC的中點
∴OD∥AC
又DE⊥AC
∴OD⊥DE
∴DE為⊙O的切線
(3)由AB=AC, ∠BAC=60°知∆ABC是等邊三角形
∵⊙O的半徑為5
∴AB=BC=10, CD=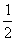 BC=5
BC=5
又∠C=60°
∴DE=CD·sin60°=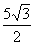
15.某校初三年級全體320名學生在電腦培訓前后各參加了一次水平相同的考試,考分都以同一標準劃分成“不及格”、“合格”、“優秀”三個等級,為了了解電腦培訓的效果,用抽簽方式得到其中64名學生的兩次考試考分等級,所繪制的統計圖如圖所示,試結合圖示信息回答下列問題:
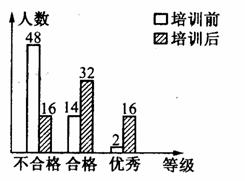
(1)這64名學生培訓前考分的中位數所在的等級是 ;
(2)估計該校整個初三年級中,培訓后考分等級為“優秀”的學生有 名;
(3)你認為上述估計合理嗎?為什么?
答: ,理由: 。
(2009年興寧市羅浮中學中考數學模擬試題,考查學生對統計圖的掌握和理解)
答案:(1)不合格 (2)80名 (3)合理,理由,利用樣本的優秀人數來詁計總體的優秀人數
14.已知點A(-2,-c)向右平移8個單位得到點 ,A與
,A與 兩點均在拋物線
兩點均在拋物線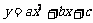 上,且這條拋物線與
上,且這條拋物線與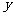 軸的交點的縱坐標為-6,求這條拋物線的頂點坐標.
軸的交點的縱坐標為-6,求這條拋物線的頂點坐標.
(2008年南通市,考查二次函數求頂點問題,綜合運用解方程組,函數圖象的平移以及二次函數的頂點式)
答案: 由拋物線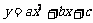 與
與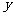 軸交點的縱坐標為-6,得
軸交點的縱坐標為-6,得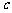 =-6.
=-6.
∴A(-2,6),點A向右平移8個單位得到點 (6,6).
(6,6).
∵A與 兩點均在拋物線上,
兩點均在拋物線上,
∴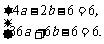 解這個方程組,得
解這個方程組,得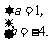
故拋物線的解析式是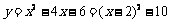 .
.
∴拋物線的頂點坐標為(2,-10).
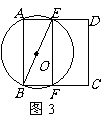
13.兩個大小不同的等腰直角三角形三角板如圖1所示放置,圖2是由它抽象出的幾何圖形,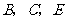 在同一條直線上,連結
在同一條直線上,連結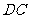 .
.

(1)請找出圖2中的全等三角形,并給予證明(說明:結論中不得含有未標識的字母);
(2)證明: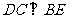 .
.
(2008年山東省泰安市,考查三角形全等的判別及學生有條理表達說理過程的能力)
答案(1)解:圖2中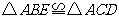
證明如下:
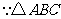 與
與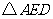 均為等腰直角三角形
均為等腰直角三角形
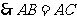 ,
,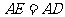 ,
,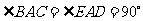
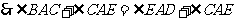
即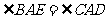
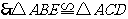
(2)證明:由(1)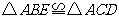 知
知
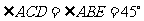
又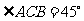
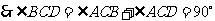
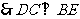
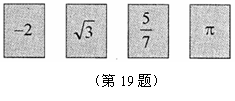
12.如圖,A,B,C,D四張卡片上分別寫有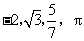 四個實數,從中任取兩張卡片.
四個實數,從中任取兩張卡片.
A B C D
(1)請列舉出所有可能的結果(用字母A,B,C,D表示);
(2)求取到的兩個數都是無理數的概率.
(2008浙江嘉興,考查概率)
答案:(1)所有可能的結果是: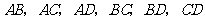 .
.
(2)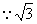 和
和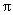 是無理數,
是無理數,
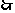 取到的兩個數都是無理數就是取到卡片
取到的兩個數都是無理數就是取到卡片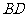 ,概率是
,概率是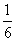 .
.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com