
2.已知函數(shù)y=f(x)的定義域?yàn)镽,且對(duì)任意a,b∈R,都有f(a+b)=f(a)+f(b),且當(dāng)x>0時(shí),f(x)<0恒成立,f(3)=-3.
(1)證明:函數(shù)y=f(x)是R上的減函數(shù);
(2)證明:函數(shù)y=f(x)是奇函數(shù);
(3)試求函數(shù)y=f(x)在[m,n](m,n∈Z)上的值域.
(1)證明 設(shè)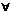 x1,x2∈R,且x1<x2,f(x2)=f[x1+(x2-x1)]=f(x1)+f(x2-x1).
x1,x2∈R,且x1<x2,f(x2)=f[x1+(x2-x1)]=f(x1)+f(x2-x1).
∵x2-x1>0,∴f(x2-x1)<0.∴f(x2)=f(x1)+f(x2-x1)<f(x1).
故f(x)是R上的減函數(shù).
(2)證明 ∵f(a+b)=f(a)+f(b)恒成立,∴可令a=-b=x,則有f(x)+f(-x)=f(0),
又令a=b=0,則有f(0)=f(0)+f(0),∴f(0)=0.從而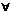 x∈R,f(x)+f(-x)=0,
x∈R,f(x)+f(-x)=0,
∴f(-x)=-f(x).故y=f(x)是奇函數(shù).
(3)解 由于y=f(x)是R上的單調(diào)遞減函數(shù),
∴y=f(x)在[m,n]上也是減函數(shù),故f(x)在[m,n]上的最大值f(x)max=f(m),最小值f(x)min=f(n).
由于f(n)=f(1+(n-1))=f(1)+f(n-1)=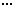 =nf(1),同理f(m)=mf(1).
=nf(1),同理f(m)=mf(1).
又f(3)=3f(1)=-3,∴f(1)=-1,∴f(m)=-m,f(n)=-n.
∴函數(shù)y=f(x)在[m,n]上的值域?yàn)椋?n,-m].
1.判斷下列各函數(shù)的奇偶性:
(1)f(x)=(x-2)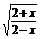 ;
;
(2)f(x)=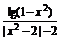 ;
;
(3)f(x)=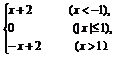
解 (1)由 ≥0,得定義域?yàn)椋?2,2),關(guān)于原點(diǎn)不對(duì)稱,故f(x)為非奇非偶函數(shù).
≥0,得定義域?yàn)椋?2,2),關(guān)于原點(diǎn)不對(duì)稱,故f(x)為非奇非偶函數(shù).
(2)由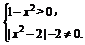 得定義域?yàn)?-1,0)∪(0,1).
得定義域?yàn)?-1,0)∪(0,1).
這時(shí)f(x)=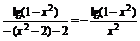 .
.
∵f(-x)=-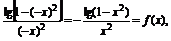 ∴f(x)為偶函數(shù).
∴f(x)為偶函數(shù).
(3)x<-1時(shí),f(x)=x+2,-x>1,
∴f(-x)=-(-x)+2=x+2=f(x).
x>1時(shí),f(x)=-x+2,
-x<-1,f(-x)=x+2=f(x).
-1≤x≤1時(shí),f(x)=0,-1≤-x≤1,
f(-x)=0=f(x).
∴對(duì)定義域內(nèi)的每個(gè)x都有f(-x)=f(x).
因此f(x)是偶函數(shù).
5.(2009·文登月考)定義域?yàn)镽的函數(shù)f(x)滿足f(-4-x)=f(x+8),且y=f(x+8)為偶函數(shù),則f(x) ( )
A.是周期為4的周期函數(shù) ? B.是周期為8的周期函數(shù)
C.是周期為12的周期函數(shù) D.不是周期函數(shù)
答案?C

例1 判斷下列函數(shù)的奇偶性.
(1)f(x)=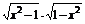 ;
;
(2)f(x)=log2(x+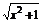 ) (x∈R);
) (x∈R);
(3)f(x)=lg|x-2|.
解 (1)∵x2-1≥0且1-x2≥0,∴x=±1,即f(x)的定義域是{-1,1}.
∵f(1)=0,f(-1)=0,∴f(1)=f(-1),f(-1)=-f(1),
故f(x)既是奇函數(shù)又是偶函數(shù).
(2)方法一 易知f(x)的定義域?yàn)镽,
又∵f(-x)=log2[-x+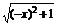 ]=log2
]=log2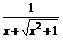 =-log2(x+
=-log2(x+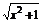 )=-f(x),
)=-f(x),
∴f(x)是奇函數(shù).
方法二 易知f(x)的定義域?yàn)镽,
又∵f(-x)+f(x)=log2[-x+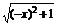 ]+log2(x+
]+log2(x+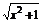 )=log21=0,即f(-x)=-f(x),
)=log21=0,即f(-x)=-f(x),
∴f(x)為奇函數(shù).
(3)由|x-2|>0,得x≠2.
∴f(x)的定義域{x|x≠2}關(guān)于原點(diǎn)不對(duì)稱,故f(x)為非奇非偶函數(shù).
例2 已知函數(shù)f(x),當(dāng)x,y∈R時(shí),恒有f(x+y)=f(x)+f(y).
(1)求證:f(x)是奇函數(shù);
(2)如果x∈R+,f(x)<0,并且f(1)=- ,試求f(x)在區(qū)間[-2,6]上的最值.
,試求f(x)在區(qū)間[-2,6]上的最值.
(1)證明 ∵函數(shù)定義域?yàn)镽,其定義域關(guān)于原點(diǎn)對(duì)稱.
∵f(x+y)=f(x)+f(y),令y=-x,∴f(0)=f(x)+f(-x).令x=y=0,
∴f(0)=f(0)+f(0),得f(0)=0.∴f(x)+f(-x)=0,得f(-x)=-f(x),
∴f(x)為奇函數(shù).
(2)解 方法一 設(shè)x,y∈R+,∵f(x+y)=f(x)+f(y),
∴f(x+y)-f(x)=f(y). ∵x∈R+,f(x)<0,
∴f(x+y)-f(x)<0, ∴f(x+y)<f(x).
∵x+y>x, ∴f(x)在(0,+∞)上是減函數(shù).
又∵f(x)為奇函數(shù),f(0)=0,
∴f(x)在(-∞,+∞)上是減函數(shù).∴f(-2)為最大值,f(6)為最小值.
∵f(1)=- ,∴f(-2)=-f(2)=-2f(1)=1,f(6)=2f(3)=2[f(1)+f(2)]=-3.
,∴f(-2)=-f(2)=-2f(1)=1,f(6)=2f(3)=2[f(1)+f(2)]=-3.
∴所求f(x)在區(qū)間[-2,6]上的最大值為1,最小值為-3.
方法二 設(shè)x1<x2,且x1,x2∈R.
則f(x2-x1)=f[x2+(-x1)]=f(x2)+f(-x1)=f(x2)-f(x1).
∵x2-x1>0,∴f(x2-x1)<0.∴f(x2)-f(x1)<0.即f(x)在R上單調(diào)遞減.
∴f(-2)為最大值,f(6)為最小值.∵f(1)=- ,
,
∴f(-2)=-f(2)=-2f(1)=1,f(6)=2f(3)=2[f(1)+f(2)]=-3.
∴所求f(x)在區(qū)間[-2,6]上的最大值為1,最小值為-3.
例3(12分)已知函數(shù)f(x)的定義域?yàn)镽,且滿足f(x+2)=-f(x)?.
(1)求證:f(x)是周期函數(shù);
(2)若f(x)為奇函數(shù),且當(dāng)0≤x≤1時(shí),f(x)= x,求使f(x)=-
x,求使f(x)=- 在[0,2
009]上的所有x的個(gè)數(shù).
在[0,2
009]上的所有x的個(gè)數(shù).
(1)證明 ∵f(x+2)=-f(x),
∴f(x+4)=-f(x+2)=-[-f(x)]=f(x), 2分
∴f(x)是以4為周期的周期函數(shù). 3分
(2)解 當(dāng)0≤x≤1時(shí),f(x)= x,
x,
設(shè)-1≤x≤0,則0≤-x≤1,∴f(-x)= (-x)=-
(-x)=- x.
x.
∵f(x)是奇函數(shù),∴f(-x)=-f(x),
∴-f(x)=- x,即f(x)=
x,即f(x)= x.
5分
x.
5分
故f(x)=  x(-1≤x≤1)
6分
x(-1≤x≤1)
6分
又設(shè)1<x<3,則-1<x-2<1,
∴f(x-2)= (x-2),
7分
(x-2),
7分
又∵f(x-2)=-f(2-x)=-f((-x)+2)=-[-f(-x)]=-f(x),
∴-f(x)= (x-2),
(x-2),
∴f(x)=- (x-2)(1<x<3).
8分
(x-2)(1<x<3).
8分
∴f(x)=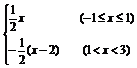 9分
9分
由f(x)=- ,解得x=-1.
,解得x=-1.
∵f(x)是以4為周期的周期函數(shù).
故f(x)=- 的所有x=4n-1 (n∈Z).
10分
的所有x=4n-1 (n∈Z).
10分
令0≤4n-1≤2 009,則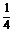 ≤n≤
≤n≤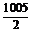 ,
,
又∵n∈Z,∴1≤n≤502 (n∈Z),
∴在[0,2 009]上共有502個(gè)x使f(x)=- .
12分
.
12分

4.已知f(x)=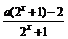 是奇函數(shù),則實(shí)數(shù)a的值等于
(
)
是奇函數(shù),則實(shí)數(shù)a的值等于
(
)
?A.1 B.-1 C.0 ?D.±1
答案?A?
3.設(shè)偶函數(shù)f(x)=loga|x-b|在(-∞,0)上單調(diào)遞增,則f(a+1)與f(b+2)的大小關(guān)系為 ( )
A.f(a+1)≥f(b+2) B.f(a+1)≤f(b+2)
C.f(a+1)<f(b+2)? D.f(a+1)>f(b+2)
答案?D?
2.已知定義在R上的奇函數(shù)f(x)滿足f(x+2)=-f(x),則f(6)的值為 ( )
?A.-1 B.0 C.1? D.2
答案?B?
1.(2008·福建理,4)函數(shù)f(x)=x3+sinx+1(x∈R),若f(a)=2,則f(-a)的值為 ( )
? A.3 ?B.0 C.-1 D.-2
答案?B?
12.已知函數(shù)y=f(x)對(duì)任意x,y∈R均有f(x)+f(y)=f(x+y),且當(dāng)x>0時(shí),f(x)<0,f(1)=-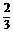 .
.
(1)判斷并證明f(x)在R上的單調(diào)性;
(2)求f(x)在[-3,3]上的最值.
解 (1)f(x)在R上是單調(diào)遞減函數(shù)
證明如下:
令x=y=0,f(0)=0,令x=-y可得:f(-x)=-f(x),在R上任取x1<x2,則x2-x1>0,
∴f(x2)-f(x1)=f(x2)+f(-x1)=f(x2-x1).又∵x>0時(shí),f(x)<0,
∴f(x2-x1)<0,即f(x2)<f(x1).由定義可知f(x)在R上為單調(diào)遞減函數(shù).
(2)∵f(x)在R上是減函數(shù),
∴f(x)在[-3,3]上也是減函數(shù).
∴f(-3)最大,f(3)最小.f(3)=f(2)+f(1)=f(1)+f(1)+f(1)=3×(-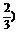 =-2.
=-2.
∴f(-3)=-f(3)=2.即f(x)在[-3,3]上最大值為2,最小值為-2.
§2.3 函數(shù)的奇偶性

 基礎(chǔ)自測
基礎(chǔ)自測
11.(2008·青島調(diào)研)已知f(x)=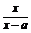 (x≠a).
(x≠a).
(1)若a=-2,試證f(x)在(-∞,-2)內(nèi)單調(diào)遞增;
(2)若a>0且f(x)在(1,+∞)內(nèi)單調(diào)遞減,求a的取值范圍.
(1)證明 任設(shè)x1<x2<-2,則f(x1)-f(x2)=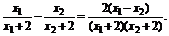
∵(x1+2)(x2+2)>0,x1-x2<0,∴f(x1)<f(x2),∴f(x)在(-∞,-2)內(nèi)單調(diào)遞增.
(2)解 任設(shè)1<x1<x2,則f(x1)-f(x2)=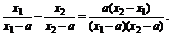
∵a>0,x2-x1>0,∴要使f(x1)-f(x2)>0,只需(x1-a)(x2-a)>0恒成立,
∴a≤1.綜上所述知0<a≤1.
10.函數(shù)f(x)對(duì)任意的實(shí)數(shù)m、n有f(m+n)=f(m)+f(n),且當(dāng)x>0時(shí)有f(x)>0.
(1)求證:f(x)在(-∞,+∞)上為增函數(shù);
(2)若f(1)=1,解不等式f[log2(x2-x-2)]<2.
(1)證明 設(shè)x2>x1,則x2-x1>0.
∵f(x2)-f(x1)=f(x2-x1+x1)-f(x1)=f(x2-x1)+f(x1)-f(x1)=f(x2-x1)>0,
∴f(x2)>f(x1),f(x)在(-∞,+∞)上為增函數(shù).
(2)解 ∵f(1)=1,∴2=1+1=f(1)+f(1)=f(2).
又f[log2(x2-x-2)]<2,∴f[log2(x2-x-2)]<f(2).
∴l(xiāng)og2(x2-x-2)<2,于是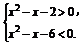 ∴
∴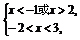
即-2<x<-1或2<x<3.∴原不等式的解集為{x|-2<x<-1或2<x<3}.
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com