
【題目】拋物線![]() (
(![]() 為常數(shù),
為常數(shù),![]() )與
)與![]() 軸交于
軸交于![]() ,
,![]() 兩點,與
兩點,與![]() 軸交于
軸交于![]() 點.設該拋物線的頂點為
點.設該拋物線的頂點為![]() ,其對稱軸與
,其對稱軸與![]() 軸的交點為
軸的交點為![]() .
.
(1)求該拋物線的解析式;
(2)![]() 為線段
為線段![]() (含端點
(含端點![]() )上一點,
)上一點,![]() 為
為![]() 軸上一點,且
軸上一點,且![]() .
.
①求![]() 的取值范圍;
的取值范圍;
②當![]() 取最大值時,將線段
取最大值時,將線段![]() 向上平移
向上平移![]() 個單位長度,使得線段
個單位長度,使得線段![]() 與拋物線有兩個交點,求
與拋物線有兩個交點,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]()
【解析】
(1)利用待定系數(shù)法將A和B的坐標代入求解即可;
(2)①拋物線的對稱軸為:x=2,頂點M(2,4),在Rt△PCQ中,由勾股定理得:PC2+PQ2=CQ2,把三角形三邊長用點P,Q的坐標表達出來,整理得:![]() ,利用0≤m≤4,求出n的取值范圍;
,利用0≤m≤4,求出n的取值范圍;
②設線段CQ向上平移t個單位長度后的解析式為:![]() 聯(lián)立拋物線方程,可求出x2-7x+4t=0,由△=49-16t=0,得
聯(lián)立拋物線方程,可求出x2-7x+4t=0,由△=49-16t=0,得![]() ,可得當線段CQ與拋物線有兩個交點時,
,可得當線段CQ與拋物線有兩個交點時,![]() .
.
解:(1)∵ 點![]() ,
,![]() 在拋物線上,
在拋物線上,
∴ ![]()
解得![]() ,
,![]() .
.
∴ 該拋物線的解析式為![]() ;
;
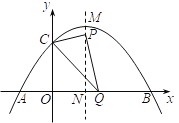
(2)① 由![]() ,得
,得![]() (2,4),
(2,4),
設![]() 點坐標為(2,m),其中
點坐標為(2,m),其中![]() ,
,
則![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴在△PCQ中,![]() ,
,
即![]() ,
,
整理得![]() ,0≤m≤4,
,0≤m≤4,
∴當![]() 時,
時,![]() 取得最小值為
取得最小值為![]() ;
;
當![]() 時,
時,![]() 取得最大值為
取得最大值為![]() ,
,
∴![]() 的取值范圍是
的取值范圍是![]() ;
;
②由①知,當![]() 取最大值4時,
取最大值4時,![]() .此時
.此時![]() ,
,
∵點![]() ,
,
∴線段![]() 的解析式為
的解析式為![]() ,
,
設![]() 向上平移
向上平移![]() 個單位長度后的解析式為
個單位長度后的解析式為![]() .
.
如圖,當線段![]() 向上平移,使點
向上平移,使點![]() 恰好在拋物線上時,線段
恰好在拋物線上時,線段![]() 與拋物線有兩個交點,此時點
與拋物線有兩個交點,此時點![]() 的坐標
的坐標![]() .
.
將![]() 代入
代入![]() ,得
,得![]() .
.
當線段![]() 繼續(xù)向上平移,線段
繼續(xù)向上平移,線段![]() 與拋物線只有一個交點時,
與拋物線只有一個交點時,
由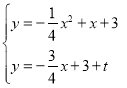 ,
,
得![]() .化簡,得
.化簡,得![]() .
.
由![]() ,解得
,解得![]() .
.
∴![]() 的取值范圍是
的取值范圍是![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數(shù)學 來源: 題型:
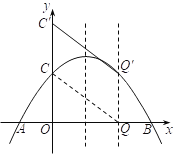
【題目】如圖,在由邊長為1個單位長度的小正方形組成的8×9的網(wǎng)格中,已知△ABC的頂點均為網(wǎng)格線的交點.
(1)在給定的網(wǎng)格中,畫出△ABC關于直線AB對稱的△ABC1.
(2)將△ABC1繞著點O旋轉(zhuǎn)后能與△ABC重合,請在網(wǎng)格中畫出點O的位置.
(3)在給定的網(wǎng)格中,畫出以點C為位似中心,將△ABC放大為原來的2倍后得到的△A2B2C.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
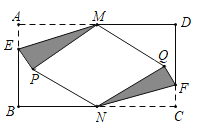
【題目】如圖, 在矩形紙片![]() 中,
中, ![]() , 點
, 點![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的中點, 點
的中點, 點![]() ,
,![]() 分別在
分別在![]() ,
,![]() 上, 且
上, 且![]() .將
.將![]() 沿
沿![]() 折疊, 點
折疊, 點![]() 的對應點為點
的對應點為點![]() ,將
,將![]() 沿
沿![]() 折疊, 點
折疊, 點![]() 的對應點為點
的對應點為點![]() ,當四邊形
,當四邊形![]() 為菱形時, 則
為菱形時, 則![]() _______.
_______.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
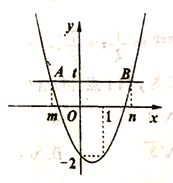
【題目】如圖為二次函數(shù)![]() 圖象,直線
圖象,直線![]() 與拋物線交于
與拋物線交于![]() 兩點,
兩點,![]() 兩點橫坐標分別為
兩點橫坐標分別為![]() 根據(jù)函數(shù)圖象信息有下列結(jié)論:
根據(jù)函數(shù)圖象信息有下列結(jié)論:
①![]() ;
;
②若對于![]() 的任意值都有
的任意值都有![]() ,則
,則![]() ;
;
③![]() ;
;
④![]() ;
;
⑤當![]() 為定值時若
為定值時若![]() 變大,則線段
變大,則線段![]() 變長
變長
其中,正確的結(jié)論有__________(寫出所有正確結(jié)論的番號)
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在每個小正方形的邊長為![]() 的網(wǎng)格中,點
的網(wǎng)格中,點![]() ,點
,點![]() 均落在格點上,
均落在格點上,![]() 為⊙
為⊙![]() 的直徑.
的直徑.
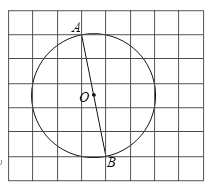
(1)![]() 的長等于__________;
的長等于__________;
(2)請在如圖所示的網(wǎng)格中,用無刻度的直尺,畫出一個以![]() 為斜邊、面積為
為斜邊、面積為![]() 的
的![]() ,并簡要說明點
,并簡要說明點![]() 的位置是如何找到的(不要求證明)__________.
的位置是如何找到的(不要求證明)__________.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】拋物線![]()
![]() 與
與![]() 軸交于
軸交于![]() ,
,![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,已知點
,已知點![]() .
.
(1)若![]() ,求
,求![]() ,
,![]() 滿足的關系式;
滿足的關系式;
(2)直線![]() 與拋物線交于
與拋物線交于![]() ,
,![]() 兩點,拋物線的對稱軸為直線
兩點,拋物線的對稱軸為直線![]() ,且
,且![]() .
.
①求拋物線的解析式(各項系數(shù)用含![]() 的式子表示);
的式子表示);
②求線段![]() 長度的取值范圍.
長度的取值范圍.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
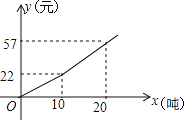
【題目】為鼓勵市民節(jié)約用水,某市自來水公司按分段收費標準收費,右圖反映的是每月收水費y(元)與用水量x(噸)之間的函數(shù)關系
(1)小紅家五月份用水8噸,應交水費_____元;
(2)按上述分段收費標準,小紅家三、四月份分別交水費36元和19.8元,問四月份比三月份節(jié)約用水多少噸?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,AB=DB,∠1=∠2,請問添加下面哪個條件不能判斷△ABC≌△DBE的是( )

A. BC=BE B. ∠A=∠D C. ∠ACB=∠DEB D. AC=DE
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com