
【題目】某中學開展“陽光體育一小時”活動,按學校實際情況,決定開設A:踢毽子;B:籃球;C:跳繩;D:乒乓球四種運動項目.為了解學生最喜歡哪一種運動項目,隨機抽取了一部分學生進行調查,并將調查結果繪制成如下兩個統計圖.請結合圖中的信息解答下列問題: 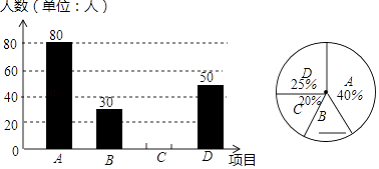
(1)本次共調查了名學生;
(2)在扇形統計圖中,“B”所在扇形的圓心角是度;
(3)將條形統計圖補充完整;
(4)若該中學有1200名學生,喜歡籃球運動的學生約有名.
【答案】
(1)200
(2)54
(3)解:C項目的人數為200×20%=40,
補全圖形為:
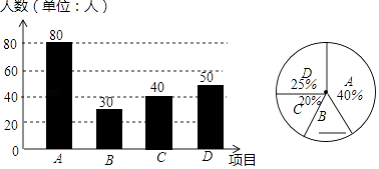
(4)180
【解析】解:(1)根據題意得:80÷40%=200(人),故本次共調查200名學生,所以答案是:200.(2)扇形統計圖中,“B”所在扇形的圓心角是360°×(1﹣40%﹣20%﹣25%)=54°,所以答案是:54;(4)“籃球”的百分比為1﹣40%﹣20%﹣25%=15%,則喜歡籃球運動的學生約有1200×15%=180(人),所以答案是:180.
【考點精析】利用扇形統計圖和條形統計圖對題目進行判斷即可得到答案,需要熟知能清楚地表示出各部分在總體中所占的百分比.但是不能清楚地表示出每個項目的具體數目以及事物的變化情況;能清楚地表示出每個項目的具體數目,但是不能清楚地表示出各個部分在總體中所占的百分比以及事物的變化情況.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
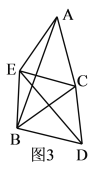
【題目】如圖已知△CAB和△CDE中,CA=CB,CD=CE,∠BCA=∠DCE=![]() .連BE,BD.
.連BE,BD.
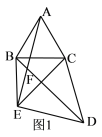
(1)如圖1,若∠BCA=60![]() ,BD與AE交于點F,求∠AFB的度數;
,BD與AE交于點F,求∠AFB的度數;
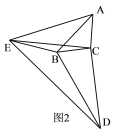
(2)如圖2,請探究∠EBD,∠AEB與![]() 之間的關系;
之間的關系;
(3)如圖3,直接寫出∠EBD,∠AEB與![]() 之間的關系.
之間的關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某地下車庫出口處安裝了“兩段式欄桿”,如圖1所示,點A是欄桿轉動的支點,點E是欄桿兩段的聯結點.當車輛經過時,欄桿AEF最多只能升起到如圖2所示的位置,其示意圖如圖3所示(欄桿寬度忽略不計),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么適合該地下車庫的車輛限高標志牌為( )(參考數據:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75) 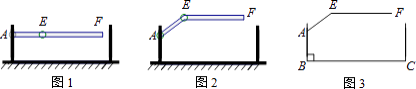
A.
B.
C.
D.
查看答案和解析>>
科目:初中數學 來源: 題型:
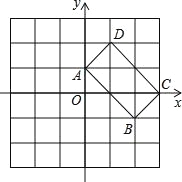
【題目】如圖,在 6×6 的網格中,四邊形 ABCD 的頂點都在格點上,每個格子都是邊長為 1 的正方形,建立如圖所示的平面直角坐標系.
(1)畫出四邊形 ABCD 關于 y 軸對稱和四邊形 A′B′C′D′(點 A、B、C、D的對稱點分別是點 A′B′C′D′.
(2)求 A、B′、B、C 四點組成和四邊形的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:直線 a,b,c 表示三條相互交叉而建的公路,現在要建立一個貨物中轉站,要求它到三條公路的距離相等,則可供選擇的地址有( )
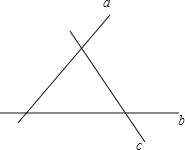
A. 1 個 B. 2 個 C. 3 個 D. 4 個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將四根長度相等的細木條首尾相接,用釘子釘成四邊形ABCD,轉動這個四邊形,使它形狀改變,當∠C=90°時,測得AC=2 ![]() ,當∠C=120°時,如圖2,AC=( )
,當∠C=120°時,如圖2,AC=( ) 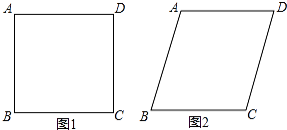
A.2
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市新建火車站廣場將投入使用,計劃在廣場內種植A,B兩種花木共4000棵,若A花木數量是B花木數量的2倍還多400棵.
(1)求A,B兩種花木的數量分別是多少棵?
(2)如果園林處安排24人同時種植這兩種花木,每人每天能種植A花木70棵或B花木60棵,應怎樣分別安排種植A花木和種植B花木的人數,才能確保同時完成各自的任務?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】目前,我市正在積極創建文明城市,交通部門一再提醒司機:為了安全,請勿超速,并再進一步完善各類監測系統,如圖,在某公路直線路段MN內限速60千米/小時,為了檢測車輛是否超速,在公路MN旁設立了觀測點C,從觀測點C測得一小車從點A到達點B行駛了5秒鐘,已知∠CAN=45°,∠CBN=60°,BC=200米,此車超速了嗎?請說明理由.(參考數據: ![]() =1.41,
=1.41, ![]() =1.73)
=1.73) 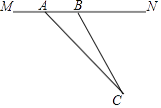
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com