【題目】某學校舉行數學競賽，需購買
兩種獎品共160件，其中
種獎品的單價為12元，
種獎品的單價為8元，且購買種獎品的數量不大于種獎品數量的3倍，假設購買種獎品的數量為
件.
（1）根據題意填空：
購買種獎品的費用為___（元）；
購買種獎品的費用為___（元）；
（2）若購買兩種獎品所需的總費用為
元，試求與的函數關系式，并求出的取值范圍；
（3）問兩種獎品各購買多少件時所需的總費用最少，并求出最少費用.
【答案】（1）
，
；（2）
，
；（3）購買
種獎品40件，
種獎品120件時，所需費用最少，最少費用為1440元．
【解析】
（1）根據總費用=單價×數量填空；
（2）根據題意可以寫出y與x的函數關系式，根據題意可以列出相應的不等式，求出x的取值范圍；
（3）根據一次函數的性質即可解答本題．
解：（1）根據題意填空：
購買種獎品的費用為 （元）；
購買種獎品的費用為（元）；
（2）根據題意得，
∴
，解得：
由題意得：
∴；
（3）∵
∴
隨
的增大而增大
∵
∴當
時，
（元）
∴當購買種獎品40件，種獎品120件時，所需費用最少，最少費用為1440元 .
故答案為：（1），；（2），；（3）購買種獎品40件，種獎品120件時，所需費用最少，最少費用為1440元．
一線名師權威作業本系列答案科目：初中數學 來源： 題型：
【題目】出租車司機小李某天上午營運時是在東西走向的大街上進行的，如果規定向東為正，向西為負，他這天上午所接六位乘客的行車里程（單位：
）如下：
，
，
，
，
，，
問：（1）將最后一位乘客送到目的地時，小李在什么位置？
（2）若汽車耗油量為
（升/千米），這天上午小李接送乘客，出租車共耗油多少升？
（3）若出租車起步價為8元，起步里程為
（包括），超過部分每千米1.2元，問小李這天上午共得車費多少元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，D是BC上一點，DE∥AB，交AC于點E，DF∥AC，交AB點F．
（1）直接寫出圖中與∠BAC構成的同旁內角．
（2）請說明∠A與∠EDF相等的理由．
（3）若∠BDE +∠CDF＝234°，求∠BAC的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小張騎自行車勻速從甲地到乙地，在途中休息了-段時間后，仍按原速行駛他距乙地的距離與時間的關系如圖中折線所示，小李騎摩托車勻速從乙地到甲地，比小張晚出發一段時間，他距乙地的距離與時間的關系如圖中線段AB所示，
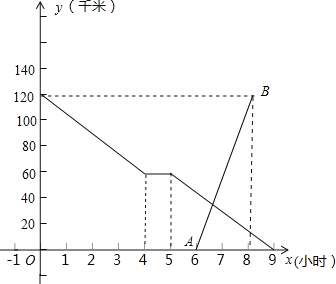
(1)小李到達甲地后，再經過 小時小張到達乙地；小張騎自行車的速度是 千米/小時；
(2)請你寫出小李距乙地的距離y(千米)與時間x(小時)之間的函數關系(不要求寫出定義域);
(3)若小李想在小張休息期間(第4小時和第5小時不算小張休息)與他相遇，則他出發的時間x應在什么范圍?(直接寫出答案)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀材料：數學課上，吳老師在求代數式x2﹣4x+5的最小值時，利用公式a2±2ab+b2=（a±b）2，對式子作如下變形：x2﹣4x+5=x2﹣4x+4+1=（x﹣2）2+1，
因為（x﹣2）2≥0，
所以（x﹣2）2+1≥1，
當x=2時，（x﹣2）2+1=1，
因此（x﹣2）2+1有最小值1，即x2﹣4x+5的最小值為1．
通過閱讀，解下列問題：
（1）代數式x2+6x+12的最小值為 ；
（2）求代數式﹣x2+2x+9的最大或最小值；
（3）試比較代數式3x2﹣2x與2x2+3x﹣7的大小，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀并回答問題．
求一元二次方程ax2+bx+c=0（a≠0）的根（用配方法）．
解：ax2+bx+c=0，
∵a≠0，∴x2+
x+
=0，第一步
移項得：x2+x=﹣，第二步
兩邊同時加上（
）2，得x2+x+（ ）2=﹣+（）2，第三步
整理得：（x+）2=
直接開方得x+=±
，第四步
∴x=
，
∴x1=
，x2=
，第五步
上述解題過程是否有錯誤？若有，說明在第幾步，指明產生錯誤的原因，寫出正確的過程；若沒有，請說明上述解題過程所用的方法．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在△ABC中,∠ACB=90°,BD是△ABC的角平分線,P是射線AC上任意一點 (不與A. D. C三點重合)，過點P作PQ⊥AB，垂足為Q，交直線BD于E.
(1)如圖①，當點P在線段AC上時，說明∠PDE=∠PED.
(2)作∠CPQ的角平分線交直線AB于點F，則PF與BD有怎樣的位置關系?畫出圖形并說明理由。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下面的文字,解答問題:大家知道
是無理數,而無理數是無限不循環小數,因此的小數部分我們不可能全部寫出來,而
＜2于是可用
來表示的小數部分.請解答下列問題：
(1)
的整數部分是_______，小數部分是_________；
(2)如果
的小數部分為
的整數部分為
求
的值；
(3)已知:
其中
是整數,且
求
的平方根。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com