【題目】在
中，
，
，
，點
、
分別在邊
、
上．如果為中點，且
，那么
的長度為__________．
【答案】5或1.4
【解析】
根據已知比例式先求出DE的長，再分兩種情況：①E為BC的中點，可直接得出AE的長；②點E在靠近點A的位置，過點D作DF⊥AC于點F，證明△ADF∽△ACB，得出
，從而可得出DF的長，再分別根據勾股定理得出AF，EF的長，從而可得出結果．
解：∵在
中，根據勾股定理得，AC=
，
又D是AB的中點，∴AD=
AB=4，
∵
，
∴
，∴DE=3．
分以下兩種情況：
①當點E在如圖①所示的位置時，即點E為AC的中點時，DE=BC=3，
故此時AE=AC=5；
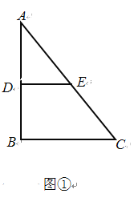
②點E在如圖②所示的位置時，DE=3，過點D作DF⊥AC于點F，
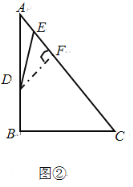
∵∠AFD=∠B=90°，∠A=∠A，
∴△ADF∽△ACB，
∴，即
，∴DF=2.4．
∴在Rt△ADF中，AF=
，
在Rt△DEF中，EF=
，
∴AE=AF-EF=1.4．
綜上所述，AE的長為5或1.4．
故答案為：5或1.4．
科目：初中數學 來源： 題型：
【題目】如圖，
個邊長為
的相鄰正方形的一邊均在同一直線上，點
，
，
，…
分別為邊
，
，
，…，
的中點，
的面積為
，
的面積為
，…
的面積為
，則
________．（用含的式子表示）
查看答案和解析>>
科目：初中數學 來源： 題型：
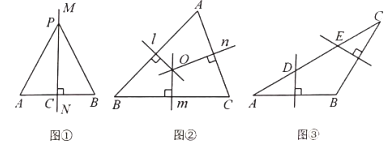
【題目】教材呈現：下圖是華師版八年級上冊數學教材第94頁的部分內容．
請根據教材中的分析，結合圖①，寫出“線段垂直平分線的性質定理”完整的證明過程．
定理應用：
（1）如圖②，在
中，直線
分別是邊AB、BC、AC的垂直平分線．求證：直線交于點
．
（2）如圖③，在中，
，邊AB的垂直平分線交AC于點D、邊BC的垂直平分線交AC于點E．若
，
，則DE的長為___________．
查看答案和解析>>
科目：初中數學 來源： 題型：
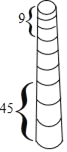
【題目】我國古代的優秀數學著作《九章算術》有一道“竹九節”問題，大意是說：現有﹣一根上細下粗共九節的竹子，自上而下從第2節開始，每一節與前一節的容積之差都相等，且最上面三節的容積共9升，最下面三節的容積共45升，求第五節的容積，及每一節與前一節的容積之差．
請解答上述問題．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系
中，已知拋物線
與
軸交于點
和點
（點在點的左側），與
軸交于點
，對稱軸是直線
．
（1）求拋物線的表達式；
（2）直線
平行于軸，與拋物線交于
、
兩點（點在點的左側），且
，點
關于直線的對稱點為
，求線段
的長；
（3）點
是該拋物線上一點，且在第一象限內，聯結
、
，交線段
于點
，當
時，求點的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
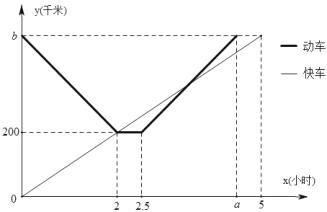
【題目】某地區在同一直線上依次有甲、乙、丙三座城市一列快車從甲市出發勻速行駛開往丙市，一列動車從丙市出發勻速行駛往返于乙、丙兩座城市，兩列火車同時出發．如圖是兩列火車距甲市的路程
（千米）與行駛時間
（小時）之間的函數圖象，請你結合圖像信息解決下列問題：
（1）直接寫出：甲、乙兩市相距 千米，圖像中
的值為 ，
的值 ；
（2）求動車從乙地返回多長時間時與快車相遇？
（3）請直接寫出快車出發多長時間兩列火車（都在行駛時）相距30千米？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，
為原點，點
，點
，點
，把
繞點順時針旋轉（旋轉角為銳角），得
，
、
、
旋轉后的對應點分別為
、
、
，
、
分別與
軸、
軸交于點
、
．
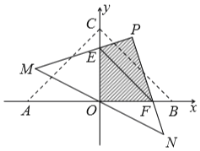
（1）求四邊形
的面積；
（2）設
，
，用含
的式子表示
；
（3）設點關于原點的對稱點為
，當
的值最小時，求的坐標．（直接寫出結果）
查看答案和解析>>
科目：初中數學 來源： 題型：
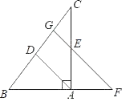
【題目】如圖，在Rt△ABC中，∠BAC＝90°，AD平分∠BAC，過AC的中點E作FG∥AD，交BA的延長線于點F，交BC于點G，
（1）求證：AE＝AF；
（2）若BC＝
AB，AF＝3，求BC的長．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
