
【題目】已知圓![]() ,
, ![]() 在拋物線
在拋物線![]() 上,圓
上,圓![]() 過原點且與
過原點且與![]() 的準線相切.
的準線相切.
(Ⅰ) 求![]() 的方程;
的方程;
(Ⅱ) 點![]() ,點
,點![]() (與
(與![]() 不重合)在直線
不重合)在直線![]() 上運動,過點
上運動,過點![]() 作
作![]() 的兩條切線,切點分別為
的兩條切線,切點分別為![]() ,
, ![]() .求證:
.求證: ![]() (其中
(其中![]() 為坐標原點).
為坐標原點).
【答案】(I)![]() ;(Ⅱ) 見解析.
;(Ⅱ) 見解析.
【解析】試題分析:(I)原點在圓上,拋物線準線與圓相切,可得![]() 三者之間的關系,進而求出
三者之間的關系,進而求出![]() 的方程;(Ⅱ) 設
的方程;(Ⅱ) 設![]() ,
, ![]() ,
, ![]() ,利用導數求得兩切線方程,利用根與系數關系可證
,利用導數求得兩切線方程,利用根與系數關系可證![]() ,即證兩角相等.
,即證兩角相等.
試題解析:(I)解法一:因為圓![]() 的圓心在拋物線上且與拋物線的準線相切,且圓半徑為
的圓心在拋物線上且與拋物線的準線相切,且圓半徑為![]() ,
,
故![]() ,
,
因為圓過原點,所以![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,
,
因為![]() ,所以
,所以![]() ,所以拋物線
,所以拋物線![]() 方程
方程![]() .
.
解法二:因為圓![]() 的圓心在拋物線上且與拋物線的準線相切,由拋物線的定義,
的圓心在拋物線上且與拋物線的準線相切,由拋物線的定義,
圓![]() 必過拋物線的焦點
必過拋物線的焦點![]() ,
,
又圓![]() 過原點,所以
過原點,所以![]() ,
,
又圓的半徑為3,所以![]() ,又
,又![]() ,
,
又![]() ,得
,得![]() ,所以
,所以![]() .所以拋物線
.所以拋物線![]() 方程
方程![]() .
.
解法三:因為圓![]() 與拋物線準線相切,所以
與拋物線準線相切,所以![]() ,
,
且圓過![]() 又圓過原點,故
又圓過原點,故![]() ,可得
,可得![]() ,
,
解得![]() ,所以拋物線
,所以拋物線![]() 方程
方程![]()
(Ⅱ) 解法一:設![]() ,
, ![]() ,
, ![]() ,
, ![]() 方程為
方程為![]() ,所以
,所以![]() , 5分
, 5分
求得拋物線在點![]() 處的切線的斜率
處的切線的斜率![]() ,所以切線
,所以切線![]() 方程為:
方程為: ![]() ,
,
即![]() ,化簡得
,化簡得![]() ,
,
又因過點![]() ,故可得,
,故可得, ![]() ,
,
即![]() ,同理可得
,同理可得![]() ,
,
所以![]() 為方程
為方程![]() 的兩根,所以
的兩根,所以![]() ,
, ![]() ,
,
因為![]() ,所以
,所以![]() ,
,
化簡![]()
![]() .
.
所以![]() .
.
解法二:依題意設點![]() ,設過點
,設過點![]() 的切線為
的切線為![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() ,即
,即![]() ,
,
不妨設切線![]() 的斜率為
的斜率為![]() ,點
,點![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,又
,又![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() ,
, ![]() ,即點
,即點![]() ,同理點
,同理點![]() ,
,
因為![]() ,所以
,所以![]() ,同理
,同理![]() ,
,
所以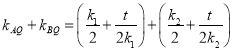
![]()
![]() ,
,
所以![]() .
.


科目:高中數學 來源: 題型:
【題目】第96屆(春季)全國糖酒商品交易會于2017年3月23日至25日在四川舉辦.展館附近一家川菜特色餐廳為了研究參會人數與本店所需原材料數量的關系,在交易會前查閱了最近5次交易會的參會人數![]() (萬人)與餐廳所用原材料數量
(萬人)與餐廳所用原材料數量![]() (袋),得到如下數據:
(袋),得到如下數據:

(Ⅰ)請根據所給五組數據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(Ⅱ)若該店現有原材料12袋,據悉本次交易會大約有13萬人參加,為了保證原材料能夠滿足需要,則該店應至少再補充原材料多少袋?
(參考公式:  ,
, ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有甲,乙,丙,丁四位同學課余參加巴蜀愛心社和巴蜀文學風的活動,每人參加且只能參加一個社團的活動,并且參加每個社團都是等可能的.
(1)求巴蜀愛心社和巴蜀文學風都至少有1人參加的概率;
(2)求甲,乙在同一個社團,丙,丁不在同一個社團的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有下列五個命題: ①平面內,到一定點的距離等于到一定直線距離的點的集合是拋物線;
②平面內,定點F1、F2 , |F1F2|=6,動點M滿足|MF1|+|MF2|=6,則點M的軌跡是橢圓;
③在△ABC中,“∠B=60°”是“∠A,∠B,∠C三個角成等差數列”的充要條件;
④“若﹣3<m<5,則方程 ![]() =1是橢圓”.
=1是橢圓”.
⑤已知向量 ![]() ,
, ![]() ,
, ![]() 是空間的一個基底,則向量
是空間的一個基底,則向量 ![]() +
+ ![]() ,
, ![]() ﹣
﹣ ![]() ,
, ![]() 也是空間的一個基底.
也是空間的一個基底.
其中真命題的序號是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四棱錐P﹣ABCD的底面為直角梯形,AB∥DC,∠DAB=90°,PA⊥底面 ABCD,且PA=AD=DB= ![]() ,AB=1,M是PB的中點.
,AB=1,M是PB的中點. 
(1)證明:面PAD⊥面PCD;
(2)求AC與PB所成的角;
(3)求平面AMC與平面BMC所成二面角的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
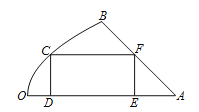
【題目】如圖是一塊地皮![]() ,其中
,其中![]() ,
, ![]() 是直線段,曲線段
是直線段,曲線段![]() 是拋物線的一部分,且點
是拋物線的一部分,且點![]() 是該拋物線的頂點,
是該拋物線的頂點, ![]() 所在的直線是該拋物線的對稱軸.經測量,
所在的直線是該拋物線的對稱軸.經測量, ![]() km,
km, ![]() km,
km, ![]() .現要從這塊地皮中劃一個矩形
.現要從這塊地皮中劃一個矩形![]() 來建造草坪,其中點
來建造草坪,其中點![]() 在曲線段
在曲線段![]() 上,點
上,點![]() ,
, ![]() 在直線段
在直線段![]() 上,點
上,點![]() 在直線段
在直線段![]() 上,設
上,設![]() km,矩形草坪
km,矩形草坪![]() 的面積為
的面積為![]() km2.
km2.
(1)求![]() ,并寫出定義域;
,并寫出定義域;
(2)當![]() 為多少時,矩形草坪
為多少時,矩形草坪![]() 的面積最大?
的面積最大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com