Question

【題目】我國是世界上嚴重缺水的國家，某市政府為了鼓勵居民節約用水，計劃調整居民生活用水收費方案，擬確定一個合理的月用水量標準（噸）、一位居民的月用水量不超過的部分按平價收費，超出的部分按議價收費.為了了解居民用水情況，通過抽樣，獲得了某年100位居民每人的月均用水量（單位：噸），將數據按照[0,0.5)，[0.5,1)，…，[4,4.5)分成9組，制成了如圖所示的頻率分布直方圖.

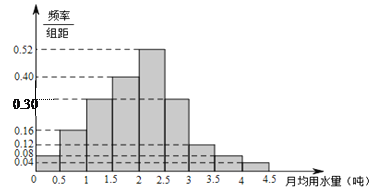
（1）設該市有30萬居民，估計全市居民中月均用水量不低于3噸的人數，并說明理由；

（2）若該市政府希望使85%的居民每月的用水量不超過標準（噸），估計的值，并說明理由.

（3）利用分層抽樣的方法在[0,0.5) [3.5,4) [4,4.5)三組中選取5位居民，再從這5位居民中任意取三人，求這三人恰有兩人來自同一組的概率。

Answer 1

【答案】（1）3.6（萬）；（2）2.9；（3）

【解析】試題分析：本題主要考查頻率分布直方圖、頻率、頻數的計算公式等基礎知識，考查學生的分析問題解決問題的能力. 第一問，由高×組距=頻率，計算每組中的頻率，因為所有頻率之和為1，計算出a的值；第二問，利用高×組距=頻率，先計算出每人月均用水量不低于3噸的頻率，再利用頻率×樣本總數=頻數，計算所求人數；第三問，將前6組的頻率之和與前5組的頻率之和進行比較，得出2.5≤x<3，再進行計算.

試題解析：（Ⅰ）由頻率分布直方圖知，月均用水量在[0,0.5)中的頻率為0.08×0.5=0.04，

同理，在[0.5,1)，[1.5,2)，[2,2.5)，[3,3.5)，[3.5,4)，[4,4.5)中的頻率分別為0.08，0.20，0.26，0.06，0.04，0.02．

由0.04+0.08+0.5×a+0.20+0.26+0.5×a+0.06+0.04+0.02=1，

解得a=0.30．

（Ⅱ）由（Ⅰ），100位居民每人月均用水量不低于3噸的頻率為0.06+0.04+0.02=0.12．

由以上樣本的頻率分布，可以估計全市30萬居民中月均用水量不低于3噸的人數為

300 000×0.12="36" 000．

（Ⅲ）因為前6組的頻率之和為0.04+0.08+0.15+0.20+0.26+0.15=0.88>0.85，

而前5組的頻率之和為0.04+0.08+0.15+0.20+0.26=0.73<0.85，

所以2.5≤x<3．

由0.3×(x–2.5)=0.85–0.73，

解得x=2.9．

所以，估計月用水量標準為2.9噸時，85%的居民每月的用水量不超過標準．