
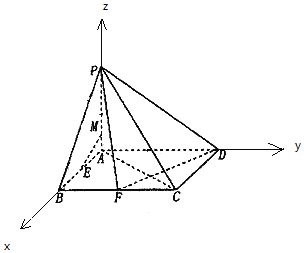
【題目】四棱錐P-ABCD的底面是邊長為2的正方形,PA⊥平面ABCD,E,F分別為線段AB,BC的中點(diǎn).
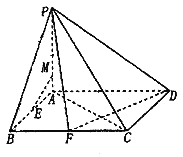
(1)線段AP上一點(diǎn)M,滿足![]() ,求證:EM∥平面PDF;
,求證:EM∥平面PDF;
(2)若PB與平面ABCD所成的角為45°,求二面角A-PD-F的余弦值.
【答案】(1)見解析(2)![]()
【解析】
(1)建立空間直角坐標(biāo)系,利用![]() ·
·![]() =0,即可證明EM∥平面PDF;
=0,即可證明EM∥平面PDF;
(2)求出平面PDF和平面PAD的一個(gè)法向量,利用向量的夾角公式,即可求解二面角的余弦值.
(1)由題意,以A為原點(diǎn),AB為x軸,AD為y軸,AP為z軸,建立空間直角坐標(biāo)系,
設(shè)PA=a,則A(0,0,0),M(0,0,![]() ),P(0,0,a),F(2,1,0),D(0,2,0),
),P(0,0,a),F(2,1,0),D(0,2,0),
E(1,0,0),所以![]() =(-1,0,
=(-1,0,![]() ),
),![]() =(2,1,-a),
=(2,1,-a),![]() =(0,2,-a),
=(0,2,-a),
設(shè)平面PDF的法向量![]() =(x,y,z),
=(x,y,z),
則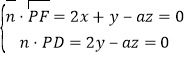 ,取z=2,得
,取z=2,得![]() =(
=(![]() ,a,2),
,a,2),
∵![]() ·
·![]() =-
=-![]() +2×
+2×![]() =0,EM
=0,EM![]() 平面PDF,∴EM∥平面PDF.
平面PDF,∴EM∥平面PDF.
(2)因?yàn)?/span>PB與平面ABCD所成的角為45°,可得PA=AB=2,
所以P(0,0,2),D(0,2,0),F(2,1,0),
所以![]() =(0,2,-2),
=(0,2,-2),![]() =(2,1,0),
=(2,1,0),
設(shè)平面PDF的法向量為![]() =(x,y,z),
=(x,y,z),
則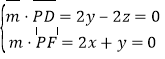 ,取y=1,得
,取y=1,得![]() =(
=(![]() ,1,1),
,1,1),
又由平面PAD的法向量![]() =(1,0,0),
=(1,0,0),
設(shè)二面角A-PD-F的平面角為θ,則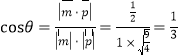 ,
,
∴二面角A-PD-F的余弦值為![]() .
.


 鷹派教輔銜接教材河北教育出版社系列答案
鷹派教輔銜接教材河北教育出版社系列答案 初中暑期銜接系列答案
初中暑期銜接系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時(shí),求函數(shù)
時(shí),求函數(shù)![]() 的單調(diào)遞增區(qū)間;
的單調(diào)遞增區(qū)間;
(2)設(shè)![]() 的內(nèi)角
的內(nèi)角![]() 的對應(yīng)邊分別為
的對應(yīng)邊分別為![]() ,且
,且![]() ,若向量
,若向量![]() 與向量
與向量![]() 共線,求
共線,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某課題小組共10人,已知該小組外出參加交流活動次數(shù)為1,2,3的人數(shù)分別為3,3, 4,現(xiàn)從這10人中隨機(jī)選出2人作為該組代表參加座談會.
(1)記“選出2人外出參加交流活動次數(shù)之和為4”為事件A,求事件A發(fā)生的概率;
(2)設(shè)X為選出2人參加交流活動次數(shù)之差的絕對值,求隨機(jī)變量X的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】隨著國家二孩政策的全面放開,為了調(diào)查一線城市和非一線城市的二孩生育意愿,某機(jī)構(gòu)用簡單隨機(jī)抽樣方法從不同地區(qū)調(diào)查了100位育齡婦女,結(jié)果如下表.
非一線城市 | 一線城市 | 總計(jì) | |
愿生 | 45 | 20 | 65 |
不愿生 | 13 | 22 | 35 |
總計(jì) | 58 | 42 | 100 |
附表:
|
|
|
|
|
|
|
|
|
|
由![]() 算得,
算得,![]() ,
,
參照附表,得到的正確結(jié)論是
A. 在犯錯(cuò)誤的概率不超過0.1%的前提下,認(rèn)為“生育意愿與城市級別有關(guān)”
B. 在犯錯(cuò)誤的概率不超過0.1%的前提下,認(rèn)為“生育意愿與城市級別無關(guān)”
C. 有99%以上的把握認(rèn)為“生育意愿與城市級別有關(guān)”
D. 有99%以上的把握認(rèn)為“生育意愿與城市級別無關(guān)”
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知a=(sinx,cosx),b=(sinx,sinx),f(x)=2a·b.
(1)求f(x)的最小正周期和最大值;
(2)若g(x)=f(x),x∈![]() ,畫出函數(shù)y=g(x)的圖象,討論y=g(x)-m(m∈R)的零點(diǎn)個(gè)數(shù).
,畫出函數(shù)y=g(x)的圖象,討論y=g(x)-m(m∈R)的零點(diǎn)個(gè)數(shù).

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了適應(yīng)高考改革,某中學(xué)推行“創(chuàng)新課堂”教學(xué).高一平行甲班采用“傳統(tǒng)教學(xué)”的教學(xué)方式授課,高一平行乙班采用“創(chuàng)新課堂”的教學(xué)方式授課,為了比較教學(xué)效果,期中考試后,分別從兩個(gè)班中各隨機(jī)抽取![]() 名學(xué)生的成績進(jìn)行統(tǒng)計(jì)分析,結(jié)果如下表:(記成績不低于
名學(xué)生的成績進(jìn)行統(tǒng)計(jì)分析,結(jié)果如下表:(記成績不低于![]() 分者為“成績優(yōu)秀”)
分者為“成績優(yōu)秀”)
分?jǐn)?shù) |
|
|
|
|
|
|
|
甲班頻數(shù) |
|
|
|
|
|
|
|
乙班頻數(shù) |
|
|
|
|
|
|
|
(Ⅰ)由以上統(tǒng)計(jì)數(shù)據(jù)填寫下面的![]() 列聯(lián)表,并判斷是否有
列聯(lián)表,并判斷是否有![]() 以上的把握認(rèn)為“成績優(yōu)秀與教學(xué)方式有關(guān)”?
以上的把握認(rèn)為“成績優(yōu)秀與教學(xué)方式有關(guān)”?
甲班 | 乙班 | 總計(jì) | |
成績優(yōu)秀 | |||
成績不優(yōu)秀 | |||
總計(jì) |
(Ⅱ)現(xiàn)從上述樣本“成績不優(yōu)秀”的學(xué)生中,抽取![]() 人進(jìn)行考核,記“成績不優(yōu)秀”的乙班人數(shù)為
人進(jìn)行考核,記“成績不優(yōu)秀”的乙班人數(shù)為![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
參考公式:![]() ,其中
,其中![]() .
.
臨界值表
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】給出以下四個(gè)說法:
①殘差點(diǎn)分布的帶狀區(qū)域的寬度越窄相關(guān)指數(shù)越小
②在刻畫回歸模型的擬合效果時(shí),相關(guān)指數(shù)![]() 的值越大,說明擬合的效果越好;
的值越大,說明擬合的效果越好;
③在回歸直線方程![]() 中,當(dāng)解釋變量
中,當(dāng)解釋變量![]() 每增加一個(gè)單位時(shí),預(yù)報(bào)變量
每增加一個(gè)單位時(shí),預(yù)報(bào)變量![]() 平均增加
平均增加![]() 個(gè)單位;
個(gè)單位;
④對分類變量![]() 與
與![]() ,若它們的隨機(jī)變量
,若它們的隨機(jī)變量![]() 的觀測值
的觀測值![]() 越小,則判斷“
越小,則判斷“![]() 與
與![]() 有關(guān)系”的把握程度越大.
有關(guān)系”的把握程度越大.
其中正確的說法是![]()
A. ①④B. ②④C. ①③D. ②③
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】CPI是居民消費(fèi)價(jià)格指數(shù)(consumer price index)的簡稱.居民消費(fèi)價(jià)格指數(shù),是一個(gè)反映居民家庭一般所購買的消費(fèi)品價(jià)格水平變動情況的宏觀經(jīng)濟(jì)指標(biāo).右圖是根據(jù)統(tǒng)計(jì)局發(fā)布的2018年1月—7月的CPI 同比增長與環(huán)比增長漲跌幅數(shù)據(jù)繪制的折線圖.(注:2018 年2月與2017年2月相比較,叫同比;2018年2 月與2018年1月相比較,叫環(huán)比)根據(jù)該折線圖,則下列結(jié)論錯(cuò)誤的是( )
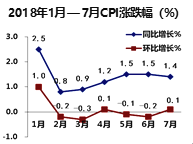
A. 2018年1月—7月CPI 有漲有跌
B. 2018年2月—7月CPI 漲跌波動不大,變化比較平穩(wěn)
C. 2018年1月—7月分別與2017年1月一7月相比較,1月CPI 漲幅最大
D. 2018年1月—7月分別與2017年1月一7月相比較,CPI 有漲有跌
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直線l過點(diǎn)P(3,4)
(1)它在y軸上的截距是在x軸上截距的2倍,求直線l的方程.
(2)若直線l與![]() 軸,
軸,![]() 軸的正半軸分別交于點(diǎn)
軸的正半軸分別交于點(diǎn)![]() ,求
,求![]() 的面積的最小值.
的面積的最小值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com