
【題目】已知函數 ![]() 為自然對數的底數.
為自然對數的底數.
(1)求曲線 ![]() 在
在 ![]() 處的切線方程;
處的切線方程;
(2)關于 ![]() 的不等式
的不等式 ![]() 在
在 ![]() 上恒成立,求實數
上恒成立,求實數 ![]() 的值;
的值;
(3)關于 ![]() 的方程
的方程 ![]() 有兩個實根
有兩個實根 ![]() ,求證:
,求證: ![]() .
.
【答案】
(1)
解:對函數 ![]() 求導得
求導得 ![]() ,
,
∴ ![]() ,
,
又 ![]() ,
,
∴曲線 ![]() 在
在 ![]() 處的切線方程為
處的切線方程為 ![]() ,即
,即 ![]() ;
;
(2)
記 ![]() ,其中
,其中 ![]() ,
,
由題意知 ![]() 在
在 ![]() 上恒成立,下求函數
上恒成立,下求函數 ![]() 的最小值,
的最小值,
對 ![]() 求導得
求導得 ![]() ,
,
令 ![]() ,得
,得 ![]() ,
,
當 ![]() 變化時,
變化時, ![]() 變化情況列表如下:
變化情況列表如下:
|
|
|
|
| - | 0 | + |
|
| 極小值 |
|
∴ ![]() ,
,
∴ ![]() ,
,
記 ![]() ,則
,則 ![]() ,
,
令 ![]() ,得
,得 ![]() .
.
當 ![]() 變化時,
變化時, ![]() 變化情況列表如下:
變化情況列表如下:
|
| 1 |
|
| + | 0 | - |
|
| 極大值 |
|
∴ ![]() ,
,
故 ![]() 當且僅當
當且僅當 ![]() 時取等號,
時取等號,
又 ![]() ,從而得到
,從而得到 ![]() ;
;
(3)
先證 ![]() ,
,
記 ![]() ,則
,則 ![]() ,
,
令 ![]() ,得
,得 ![]() ,
,
當 ![]() 變化時,
變化時, ![]() 變化情況列表如下:
變化情況列表如下:
|
|
|
|
| - | 0 | + |
|
| 極小值 |
|
∴ ![]() ,
,
![]() 恒成立,即
恒成立,即 ![]() ,
,
記直線 ![]() 分別與
分別與 ![]() 交于
交于 ![]() ,
,
不妨設 ![]() ,則
,則 ![]() ,
,
從而 ![]() ,當且僅當
,當且僅當 ![]() 時取等號,
時取等號,
由(2)知, ![]() ,則
,則 ![]() ,
,
從而 ![]() ,當且僅當
,當且僅當 ![]() 時取等號,
時取等號,
故 ![]() ,
,
因等號成立的條件不能同時滿足,故 ![]() .
.
【解析】(1)利用導數求切線方程;(2)設 ![]() ,將題目轉化為g(x)≥0在(0,+∞)上恒成立,然后討論g(x)的單調性,表示出其最小值,其最小值大于等于0即可;(3)先證
,將題目轉化為g(x)≥0在(0,+∞)上恒成立,然后討論g(x)的單調性,表示出其最小值,其最小值大于等于0即可;(3)先證 ![]() ,設
,設 ![]() ,根據h(x)的單調性求出最小值,得h(x)恒大于零,即
,根據h(x)的單調性求出最小值,得h(x)恒大于零,即 ![]() 。記直線
。記直線 ![]() 分別與
分別與 ![]() 交于
交于 ![]() ,令
,令 ![]() ,則
,則 ![]() ,得
,得 ![]() ,因等號成立的條件不能同時滿足,故
,因等號成立的條件不能同時滿足,故 ![]() .
.
【考點精析】解答此題的關鍵在于理解利用導數研究函數的單調性的相關知識,掌握一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減.
在這個區間單調遞減.


科目:高中數學 來源: 題型:
【題目】若n是一個三位正整數,且n的個位數字大于十位數字,十位數字大于百位數字,則稱n為“三位遞增數”(如137,359,567等).在某次數學趣味活動中,每位參加者需從所有的“三位遞增數”中隨機抽取1個數,且只能抽取一次.得分規則如下:若抽取的“三位遞增數”的三個數字之積不能被5整除,參加者得0分;若能被5整除,但不能被10整除,得-1分;若能被10整除,得1分.
(1)寫出所有個位數字是5的“三位遞增數” ;
(2)若甲參加活動,求甲得分X的分布列和數學期望EX.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,點
,點![]() 和點
和點![]() 都在橢圓
都在橢圓![]() 上,直線
上,直線![]() 交x軸于點M.
交x軸于點M.
(1)(Ⅰ)求橢圓C的方程,并求點M的坐標(用![]() ,
,![]() 表示);
表示);
(2)(Ⅱ)設![]() 為原點,點
為原點,點![]() 與點
與點![]() 關于
關于![]() 軸對稱,直線
軸對稱,直線![]() 交X軸于點N.問:Y軸上是否存在點Q,使得
交X軸于點N.問:Y軸上是否存在點Q,使得![]() ?若存在,求點
?若存在,求點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足a1=1,an+1=3an+1.
(1)證明{an+ ![]() }是等比數列,并求{an}的通項公式;
}是等比數列,并求{an}的通項公式;
(2)證明: ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C1: ![]() =1(a>b>0)的離心率e=
=1(a>b>0)的離心率e= ![]() ,且過點
,且過點 ![]() ,直線l1:y=kx+m(m>0)與圓C2:(x﹣1)2+y2=1相切且與橢圓C1交于A,B兩點. (Ⅰ)求橢圓C1的方程;
,直線l1:y=kx+m(m>0)與圓C2:(x﹣1)2+y2=1相切且與橢圓C1交于A,B兩點. (Ⅰ)求橢圓C1的方程;
(Ⅱ)過原點O作l1的平行線l2交橢圓于C,D兩點,設|AB|=λ|CD|,求λ的最小值.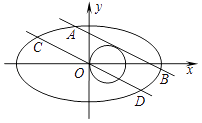
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知甲、乙兩個容器,甲容器容量為x,裝滿純酒精,乙容器容量為z,其中裝有體積為y的水(x,y<z,單位:L).現將甲容器中的液體倒入乙容器中,直至甲容器中液體倒完或乙容器盛滿,攪拌使乙容器中兩種液體充分混合,再將乙容器中的液體倒入甲容器中直至倒滿,攪拌使甲容器中液體充分混合,如此稱為一次操作,假設操作過程中溶液體積變化忽略不計.設經過n(n∈N*)次操作之后,乙容器中含有純酒精an(單位:L),下列關于數,列{an}的說法正確的是( )
A.當x=y=a時,數列{an}有最大值 ![]()
B.設bn=an+1﹣an(n∈N*),則數列{bn}為遞減數列
C.對任意的n∈N* , 始終有 ![]()
D.對任意的n∈N* , 都有 ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線l的參數方程為 ![]() (t為參數),以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C的極坐標方程為ρ2=
(t為參數),以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C的極坐標方程為ρ2= ![]() ,且直線l經過曲線C的左焦點F. ( I )求直線l的普通方程;
,且直線l經過曲線C的左焦點F. ( I )求直線l的普通方程;
(Ⅱ)設曲線C的內接矩形的周長為L,求L的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com