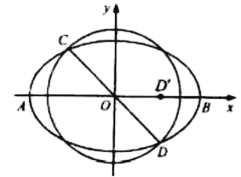
【題目】如圖，已知AB為橢圓E：
（a＞b＞0）的長軸，過坐標原點O且傾斜角為135°的直線交橢圓E于C，D兩點，且D在x軸上的射影D'恰為橢圓E的長半軸OB的中點．
（1）求橢圓E的離心率；
（2）若AB＝8，不過第四象限的直線l與橢圓E和以CD為直徑的圓均相切，求直線l的方程．
【答案】（1）
（2）
【解析】
(1) CD的方程為y = -x因為D在x軸上的射影
恰恰為橢圓E的長半軸OB的中點，所以
，代入橢圓方程得到
進而得到離心率；（2）因為AB = 8，所以2a = 8，即a = 4.由（1）知，
從而得到圓和橢圓的方程，直線l與以CD為直徑的圓相切，所以
，即
，聯立直線l和橢圓E的方程組，并消去y整理得：
，因為直線l與橢圓E相切，所以，
，化簡得，
解出參數值即可.
（1）因為直線CD過原點O且傾斜角為135°，
所以CD的方程為y = -x.
因為D在x軸上的射影恰恰為橢圓E的長半軸OB的中點，
所以.
代入橢圓E：
得，.
所以橢圓E的離心率
.
（2）因為AB = 8，所以2a = 8，即a = 4.由（1）知，.
從而橢圓E：
，以CD為直徑的圓：
.
設直線l的方程為：
.
因為直線l與以CD為直徑的圓相切，所以，即. ①
聯立直線l和橢圓E的方程組，并消去y整理得：.
因為直線l與橢圓E相切，所以，.
化簡得，. ②
由①②得，
，
，所以直線l的方程為.
新思維假期作業暑假吉林大學出版社系列答案
藍天教育暑假優化學習系列答案科目：高中數學 來源： 題型：
【題目】某電子科技公司由于產品采用最新技術，銷售額不斷增長，最近
個季度的銷售額數據統計如下表（其中
表示
年第一季度，以此類推）：
季度 |
|
|
|
|
|
季度編號x |
|
|
|
|
|
銷售額y（百萬元） |
|
|
|
|
|
（1）公司市場部從中任選
個季度的數據進行對比分析，求這個季度的銷售額都超過
千萬元的概率；
（2）求
關于
的線性回歸方程，并預測該公司
的銷售額.
附：線性回歸方程：
其中
，
參考數據：
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某小型企業甲產品生產的投入成本x（單位：萬元）與產品銷售收入y（單位：萬元）存在較好的線性關系，下表記錄了最近5次該產品的相關數據.
x（萬元） | 3 | 5 | 7 | 9 | 11 |
y（萬元） | 8 | 10 | 13 | 17 | 22 |
（1）求y關于x的線性回歸方程；
（2）根據（1）中的回歸方程，判斷該企業甲產品投入成本12萬元的毛利率更大還是投入成本15萬元的毛利率更大（毛利率
）？
相關公式：
，
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列說法中正確的個數是_________.
（1）命題“若
，則方程
有實數根”的逆否命題為“若方程無實數根，則
”.
（2）命題“
，
”的否定“
，”.
（3）若
為假命題，則
，
均為假命題.
（4）“
”是“直線
：
與直線
：
平行”的充要條件.
查看答案和解析>>
科目：高中數學 來源： 題型：
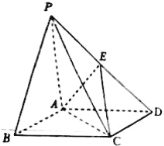
【題目】如圖，在四棱錐P—ABCD中，底面ABCD是菱形，∠ABC＝60°，PA＝AC，PB＝PD＝
AC，E是PD的中點，求證：
（1）PB∥平面ACE；
（2）平面PAC⊥平面ABCD．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下面四個命題中真命題的是（ ）
①在回歸分析模型中，殘差平方和越大，說明模型的擬合效果越好；
②兩個隨機變量相關性越強，則相關系數的絕對值越接近于1；
③在回歸直線方程
中，當解釋變量
每增加一個單位時，預報變量平均增加0.4個單位；
④對分類變量
與
的隨機變量
的觀測值
來說，越小，“與有關系”的把握程度越大.
A.①④B.②④C.①③D.②③
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，正方體
的棱長為
， 
分別是
的中點，點
在棱
上， 
（
）.
（Ⅰ）三棱錐
的體積分別為
，當
為何值時， 
最大？最大值為多少？
（Ⅱ）若
平面
，證明：平面
平面
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
.
（Ⅰ）若曲線
在點
處的切線與直線
垂直，求實數
的取值；
（Ⅱ）求函數的單調區間；
（Ⅲ）記
.當
時，函數
在區間
上有兩個零點，求實數
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
