【題目】已知f(x)是R上的奇函數，當x＞0時，解析式為f(x)＝
.
(1)求f(x)在R上的解析式；
(2)用定義證明f(x)在(0，＋∞)上為減函數．
【答案】(1) f(x)＝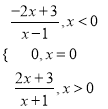
(2)見解析
【解析】試題分析：（1）分別求出當x＜0和x=0時的解析式，寫成分段函數的形式；（2）設x1，x2∈(0，＋∞)，且x1＜x2，通過作差證明f(x1)＞f(x2)即可。
試題解析：(1)設x＜0，則－x＞0，
∴f(－x)＝
.
又∵f(x)是R上的奇函數，
∴f(－x)＝－f(x)＝，
∴f(x)＝
.
又∵奇函數在x=0時有意義，
∴f(0)＝0，
∴函數的解析式為f(x)＝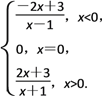
(2)證明：設x1，x2∈(0，＋∞)，且x1＜x2，
則f(x1)－f(x2)＝
－
＝
＝
.
∵x1，x2∈(0，＋∞)，x1＜x2，
∴x1＋1＞0，x2＋1＞0，x2－x1＞0，
∴f(x1)－f(x2)＞0，
∴f(x1)＞f(x2)，
∴函數f(x)在(0，＋∞)上為減函數．
教材全解字詞句篇系列答案科目：高中數學 來源： 題型：
【題目】A，B兩城相距100 km，在兩地之間距A城x km處的D地建一核電站給A，B兩城供電．為保證城市安全，核電站與城市距離不得少于10 km.已知供電費用與供電距離的平方和供電量之積成正比，比例系數λ＝0.25.若A城供電量為20億度/月，B城為10億度/月．
(1)求x的取值范圍；
(2)把月供電總費用y表示成x的函數；
(3)核電站建在距A城多遠，才能使供電費用最小？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}的通項公式是an＝
.
(1) 判斷
是不是數列{an}中的一項；
(2) 試判斷數列{an}中的項是否都在區間(0，1)內；
(3) 在區間
內有無數列{an}中的項？若有，是第幾項？若沒有，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在平面直角坐標系
中，曲線
過點
，其參數方程為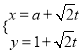
（
為參數， 
），以
為極點， 
軸非負半軸為極軸，建立極坐標系，曲線
的極坐標方程為
.
（1）求曲線
的普通方程和曲線
的直角坐標方程；
（2）已知曲線
與曲線
交于
兩點，且
，求實數
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)＝
為奇函數．
(1)求b的值；
(2)證明：函數f(x)在區間(1，＋∞)上是減函數；
(3)解關于x的不等式f(1＋x2)＋f(－x2＋2x－4)＞0.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一企業從某條生產線上隨機抽取100件產品，測量這些產品的某項技術指標值x，得到如下的頻率分布表：
x | [11，13） | [13，15） | [15，17） | [17，19） | [19，21） | [21，23） |
頻數 | 2 | 12 | 34 | 38 | 10 | 4 |
（Ⅰ）作出樣本的頻率分布直方圖，并估計該技術指標值x的平均數和眾數；
（Ⅱ）若x＜13或x≥21，則該產品不合格．現從不合格的產品中隨機抽取2件，求抽取的2件產品中技術指標值小于13的產品恰有一件的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】滬昆高速鐵路全線2016年12月28日開通運營．途經鷹潭北站的
、
兩列列車乘務組工作人員為了了解乘坐本次列車的乘客每月需求情況，分別在兩個車次各隨機抽取了100名旅客進行調查，下面是根據調查結果，繪制了月乘車次數的頻率分布直方圖和頻數分布表．
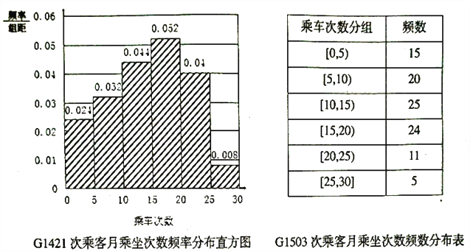
（1）若將頻率視為概率，月乘車次數不低于15次的稱之為“老乘客”，試問：哪一車次的“老乘客”較多，簡要說明理由；
（2）已知在次列車隨機抽到的50歲以上人員有35名，其中有10名是“老乘客”，由條件完成
列聯表，并根據資料判斷，是否有
的把握認為年齡與乘車次數有關，說明理由．
老乘客 | 新乘客 | 合計 | |
50歲以上 | |||
50歲以下 | |||
合計 |
附：隨機變量
（其中
為樣本容量）
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
