【題目】已知數列
滿足
，
．
（1）求證：數列
是等差數列，并求數列的通項公式；
（2）記
，
為數列
的前
項和，若
對任意的正整數都成立，求實數
的最小值．
小學期末沖刺100分系列答案
期末復習檢測系列答案
超能學典單元期中期末專題沖刺100分系列答案
黃岡360度定制密卷系列答案科目：高中數學 來源： 題型：
【題目】已知兩個不相等的非零向量
與
，兩組向量
，
，
，
，
和
，
，
，
，
均有2個和3個按照某種順序排成一列所構成，記
，且
表示
所有可能取值中的最小值，有以下結論：①有5個不同的值；②若
，則與
無關；③ 若∥，則與
無關；④ 若
，則
；⑤若
，且
，則與的夾角為
；正確的結論的序號是（ ）
A.①②④B.②④C.②③D.①⑤
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了測量某塔的高度，某人在一條水平公路
兩點進行測量.在
點測得塔底
在南偏西
，塔頂仰角為
，此人沿著南偏東
方向前進10米到
點，測得塔頂的仰角為
，則塔的高度為（ ）
A. 5米B. 10米C. 15米D. 20米
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某單位有員工1000名，平均每人每年創造利潤10萬元．為增加企業競爭力，決定優化產業結構，調整出
名員工從事第三產業，調整后平均每人每年創造利潤為
萬元
，剩下的員工平均每人每年創造的利潤可以提高
．
（1）若要保證剩余員工創造的年總利潤不低于原來1000名員工創造的年總利潤，則最多調整出多少名員工從事第三產業？
（2）若要保證剩余員工創造的年總利潤不低于原來1000名員工創造的年總利潤條件下，若要求調整出的員工創造出的年總利潤始終不高于剩余員工創造的年總利潤，則
的取值范圍是多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某企業生產某種商品
噸，此時所需生產費用為（
）萬元，當出售這種商品時，每噸價格為
萬元，這里
（
為常數，
）
（1）為了使這種商品的生產費用平均每噸最低，那么這種商品的產量應為多少噸？
（2）如果生產出來的商品能全部賣完，當產量是120噸時企業利潤最大，此時出售價格是每噸160萬元，求的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】給出以下命題，
①命題“若
，則
或
”為真命題；
②命題“若
，則
”的否命題為真命題；
③若平面
上不共線的三個點到平面
距離相等，則
④若，是兩個不重合的平面，直線
，命題
，命題
，則
是
的必要不充分條件；
⑤平面過正方體
的三個頂點
，且與底面
的交線為
，則∥
；
其中，真命題的序號是______
查看答案和解析>>
科目：高中數學 來源： 題型：
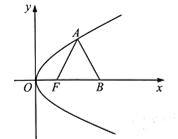
【題目】在平面直角坐標系
中，已知點F為拋物線
的焦點，點A在拋物線E上，
點B在x軸上，且
是邊長為2的等邊三角形。
（1）求拋物線E的方程；
（2）設C是拋物線E上的動點，直線
為拋物線E在點C處的切線，求點B到直線距離的最小值，并求此時點C的坐標。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
