
【題目】已知函數f(x)=xlnx,則( )
A.f(x)在(0,+∞)上是增函數
B.f(x)在 ![]() 上是增函數
上是增函數
C.當x∈(0,1)時,f(x)有最小值 ![]()
D.f(x)在定義域內無極值
科目:高中數學 來源: 題型:
【題目】對于函數f(x),若在定義域內存在實數x,滿足f(﹣x)=﹣f(x),則稱f(x)為“局部奇函數”. (I) 已知二次函數f(x)=ax2+2bx﹣3a(a,b∈R),試判斷f(x)是否為“局部奇函數”?并說明理由;
(II) 設f(x)=2x+m﹣1是定義在[﹣1,2]上的“局部奇函數”,求實數m的取值范圍;
(III) 設f(x)=4x﹣m2x+1+m2﹣3,若f(x)不是定義域R上的“局部奇函數”,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知F是拋物線y2=x的焦點,A,B是該拋物線上的兩點,|AF|+|BF|=3,則線段AB的中點到y(tǒng)軸的距離為( )
A.![]()
B.1
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐P﹣ABC中,∠APB=∠BPC=∠APC=90°,O在△ABC內,∠OPC=45°,∠OPA=60°,則∠OPB的余弦值為( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,拋物線關于x軸對稱,它的頂點在坐標原點,點P(1,2),A(x1 , y1),B(x2 , y2)均在拋物線上. 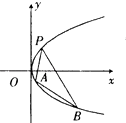
(1)求該拋物線方程;
(2)若AB的中點坐標為(1,﹣1),求直線AB方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a為實數,函數f(x)=ex﹣2x+2a,x∈R.
(1)求函數f(x)的極值;
(2)求證:當a>ln2﹣1且x>0時,ex>2x﹣2a.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=alnx+ ![]() +x(a>0).若曲線y=f(x)在點(1,f(1))處的切線與直線x﹣2y=0垂直, (Ⅰ)求實數a的值;
+x(a>0).若曲線y=f(x)在點(1,f(1))處的切線與直線x﹣2y=0垂直, (Ⅰ)求實數a的值;
(Ⅱ)求函數f(x)的單調區(qū)間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義域是一切實數的函數y=f(x),其圖象是連續(xù)不斷的,且存在常數λ(λ∈R)使得f(x+λ)+λf(x)=0對任意實數x都成立,則稱f(x)實數一個“λ一半隨函數”,有下列關于“λ一半隨函數”的結論:①若f(x)為“1一半隨函數”,則f(0)=f(2);②存在a∈(1,+∞)使得f(x)=ax為一個“λ一半隨函數;③“ ![]() 一半隨函數”至少有一個零點;④f(x)=x2是一個“λ一班隨函數”;其中正確的結論的個數是( )
一半隨函數”至少有一個零點;④f(x)=x2是一個“λ一班隨函數”;其中正確的結論的個數是( )
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com