
【題目】定義域是一切實數的函數y=f(x),其圖象是連續不斷的,且存在常數λ(λ∈R)使得f(x+λ)+λf(x)=0對任意實數x都成立,則稱f(x)實數一個“λ一半隨函數”,有下列關于“λ一半隨函數”的結論:①若f(x)為“1一半隨函數”,則f(0)=f(2);②存在a∈(1,+∞)使得f(x)=ax為一個“λ一半隨函數;③“ ![]() 一半隨函數”至少有一個零點;④f(x)=x2是一個“λ一班隨函數”;其中正確的結論的個數是( )
一半隨函數”至少有一個零點;④f(x)=x2是一個“λ一班隨函數”;其中正確的結論的個數是( )
A.1個
B.2個
C.3個
D.4個
【答案】C
【解析】解:①、若f(x)為“1一半隨函數”,則f(x+1)+f(x)=0,可得f(x+1)=﹣f(x),
可得f(x+2)=﹣f(x+1)=f(x),因此x=0,可得f(0)=f(2);故①正確;
②、假設f(x)=ax是一個“λ一半隨函數”,則ax+λ+λax=0對任意實數x成立,
則有aλ+λ=0,而此式有解,所以f(x)=ax是“λ一半隨函數”,故②正確.
③、令x=0,得f( ![]() )+
)+ ![]() f(0)=0.所以f(
f(0)=0.所以f( ![]() )=﹣
)=﹣ ![]() f(0),
f(0),
若f(0)=0,顯然f(x)=0有實數根;若f(0)≠0,f( ![]() )f(0)=﹣
)f(0)=﹣ ![]() (f(0))2<0,
(f(0))2<0,
又因為f(x)的函數圖象是連續不斷,所以f(x)在(0, ![]() )上必有實數根,
)上必有實數根,
因此任意的“﹣ ![]() 一半隨函數”必有根,即任意“﹣
一半隨函數”必有根,即任意“﹣ ![]() 一半隨函數”至少有一個零點.故③正確.
一半隨函數”至少有一個零點.故③正確.
④、假設f(x)=x2是一個“λ一半隨函數”,則(x+λ)2+λx2=0,
即(1+λ)x2+2λx+λ2=0對任意實數x成立,所以λ+1=2λ=λ2=0,而此式無解,所以f(x)=x2不是一個“λ﹣同伴函數”.故④錯誤
正確判斷:①②③.
故選:C.


 快樂5加2金卷系列答案
快樂5加2金卷系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=xlnx,則( )
A.f(x)在(0,+∞)上是增函數
B.f(x)在 ![]() 上是增函數
上是增函數
C.當x∈(0,1)時,f(x)有最小值 ![]()
D.f(x)在定義域內無極值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數f(x)=﹣ ![]() x2+bln(x+2)在區間[﹣1,2]不單調,則b的取值范圍是( )
x2+bln(x+2)在區間[﹣1,2]不單調,則b的取值范圍是( )
A.(﹣∞,﹣1]
B.[8,+∞)
C.(﹣∞,﹣1]∪[8,+∞)
D.(﹣1,8)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=1﹣ ![]() 為定義在R上的奇函數.
為定義在R上的奇函數.
(1)試判斷函數的單調性,并用定義加以證明;
(2)若關于x的方程f(x)=m在[﹣1,1]上有解,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C的對邊分別是a,b,c,若(2a﹣c)cosB=bcosC.
(1)求角B的大小,
(2)若a=3,△ABC的面積為 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,四棱錐P﹣ABCD中平面PAB⊥平面ABCD,底面ABCD是正方形.點M是棱PC的中點 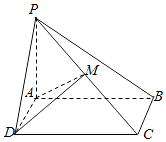
(1)記平面ADM與平面PBC的交線是l,試判斷直線l與BC的位置關系,并加以證明.
(2)若 ![]() ,求證PB⊥平面ADM,并求直線PC與平面ADM所成角的正弦值.
,求證PB⊥平面ADM,并求直線PC與平面ADM所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=4cosxsin(x+ ![]() )﹣1, (Ⅰ)求f(x)的單調遞增區間
)﹣1, (Ⅰ)求f(x)的單調遞增區間
(Ⅱ)若sin2x+af(x+ ![]() )+1>6cos4x對任意x∈(﹣
)+1>6cos4x對任意x∈(﹣ ![]() ,
, ![]() )恒成立,求實數a的取值范圍.
)恒成立,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com