
【題目】據統計,2016年“雙十”天貓總成交金額突破1207億元.某購物網站為優化營銷策略,對11月11日當天在該網站進行網購消費且消費金額不超過1000元的1000名網購者(其中有女性800名,男性200名)進行抽樣分析.采用根據性別分層抽樣的方法從這1000名網購者中抽取100名進行分析,得到下表:(消費金額單位:元)
女性消費情況:
消費金額 |
|
|
|
|
|
人數 | 5 | 10 | 15 | 47 |
|
男性消費情況:
消費金額 |
|
|
|
|
|
人數 | 2 | 3 | 10 |
| 2 |
(1)計算![]() ,
,![]() 的值;在抽出的100名且消費金額在
的值;在抽出的100名且消費金額在![]() (單位:元)的網購者中隨機選出兩名發放網購紅包,求選出的兩名網購者恰好是一男一女的概率;
(單位:元)的網購者中隨機選出兩名發放網購紅包,求選出的兩名網購者恰好是一男一女的概率;
(2)若消費金額不低于600元的網購者為“網購達人”,低于600元的網購者為“非網購達人”,根據以上統計數據填寫![]() 列聯表,并回答能否在犯錯誤的概率不超過0.010的前提下認為“是否為‘網購達人’與性別有關?”
列聯表,并回答能否在犯錯誤的概率不超過0.010的前提下認為“是否為‘網購達人’與性別有關?”
女性 | 男性 | 總計 | |
網購達人 | |||
非網購達人 | |||
總計 |
附:
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
(![]() ,其中
,其中![]() )
)
【答案】(1)![]() (2)能
(2)能
【解析】試題分析:(1)根據分層抽樣方法求出![]() 的值,利用列舉法計算基本事件數,求出對應的概率;(2)列出2×2列聯表,計算觀測值
的值,利用列舉法計算基本事件數,求出對應的概率;(2)列出2×2列聯表,計算觀測值![]() ,對照表中數據,判斷結論是否成立即可.
,對照表中數據,判斷結論是否成立即可.
(1)依題意,女性應抽取80名,男性應抽取20名,
所以![]() ,
,![]() .
.
設抽出的100名且消費金額在![]() (單位:元)的網購者中有三位女性記為
(單位:元)的網購者中有三位女性記為![]() ,
,![]() ,
,![]() ;兩位男性記為
;兩位男性記為![]() ,
,![]() ,從5人中任選2人的基本事件有:
,從5人中任選2人的基本事件有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共10個.
共10個.
設“選出的兩名網購者恰好是一男一女”為事件![]() ,事件
,事件![]() 包含的基本事件有:
包含的基本事件有:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共6件,∴
共6件,∴![]() .
.
(2)![]() 列聯表如表所示:
列聯表如表所示:
女性 | 男性 | 總計 | |
網購達人 | 50 | 5 | 55 |
非網購達人 | 30 | 15 | 45 |
總計 | 80 | 20 | 100 |
則![]() ,
,
因為![]() ,所以能在犯錯誤的概率不超過0.010的前提下認為“是否為‘網購達人’”與性別有關.
,所以能在犯錯誤的概率不超過0.010的前提下認為“是否為‘網購達人’”與性別有關.


科目:高中數學 來源: 題型:
【題目】如圖,點P在△ABC內,AB=CP=2,BC=3,∠P+∠B=π,記∠B=α. 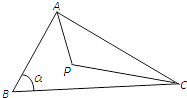
(1)試用α表示AP的長;
(2)求四邊形ABCP的面積的最大值,并寫出此時α的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,平面ABC⊥平面BCDE,BC∥DE, ![]() ,BE=CD=2,AB⊥BC,M,N分別為DE,AD中點.
,BE=CD=2,AB⊥BC,M,N分別為DE,AD中點. 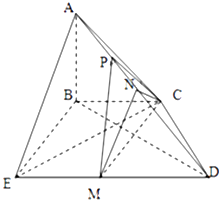
(1)證明:平面MNC⊥平面BCDE;
(2)若EC⊥CD,點P為棱AD的三等分點(近A),平面PMC與平面ABC所成銳二面角的余弦值為 ![]() ,求棱AB的長度.
,求棱AB的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,AB=AC=AD,AH⊥CD于H,BD交AH于P,且PC⊥BC 
(1)求證:A,B,C,P四點共圓;
(2)若∠CAD= ![]() ,AB=1,求四邊形ABCP的面積.
,AB=1,求四邊形ABCP的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=loga ![]() ,(a>0且a≠1).
,(a>0且a≠1).
(1)判斷f(x)的奇偶性,并加以證明;
(2)是否存在實數m使得f(x+2)+f(m﹣x)為常數?若存在,求出m的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數y= ![]() 的定義域是( )
的定義域是( )
A.[﹣ ![]() ,﹣1)∪(1,
,﹣1)∪(1, ![]() ]
]
B.(﹣ ![]() ,﹣1)∪(1,
,﹣1)∪(1, ![]() )??
)??
C.[﹣2,﹣1)∪(1,2]
D.(﹣2,﹣1)∪(1,2)
查看答案和解析>>
科目:高中數學 來源: 題型:
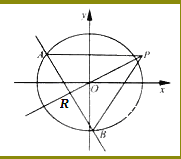
【題目】如圖,橢圓C: ![]() (a>b>0)的離心率為
(a>b>0)的離心率為![]() ,其左焦點到點
,其左焦點到點![]() 的距離為
的距離為![]() .不過原點O的直線
.不過原點O的直線![]() 與C相交于A,B兩點,且線段AB被直線OP平分.
與C相交于A,B兩點,且線段AB被直線OP平分.
(1)求橢圓C的方程;
(2)求![]() ABP的面積取最大時直線l的方程.
ABP的面積取最大時直線l的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com