【題目】已知函數(shù)f（x）=m﹣|x﹣2|，m∈R，且f（x+2）≥0的解集為[﹣1，﹣1]．
（1）求m的值；
（2）若a，b，c∈R，且 
+ 
+ 
=m，求證：a2+b2+c2≥36．
【答案】
（1）解：函數(shù)f（x）=m﹣|x﹣2|，m∈R，
故 f（x+2）=m﹣|x|，由題意可得m﹣|x|≥0的解集為[﹣1，1]，
即|x|≤m 的解集為[﹣1，1]，故m=1
（2）證明：由（1）得： 
+ 
+ 
=1，
由柯西不等式可得：
（ + + ）（a2+b2+c2）≥（1+2+3）2=36，
故a2+b2+c2≥36
【解析】（1）根據(jù)不等式的性質(zhì)得到|x|≤m 的解集為[﹣1，1]，求出m的值即可；（2）根據(jù)柯西不等式的性質(zhì)證明即可．
【考點精析】本題主要考查了基本不等式和絕對值不等式的解法的相關(guān)知識點，需要掌握基本不等式：
,（當(dāng)且僅當(dāng)
時取到等號）；變形公式：
；含絕對值不等式的解法：定義法、平方法、同解變形法，其同解定理有；規(guī)律：關(guān)鍵是去掉絕對值的符號才能正確解答此題．
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖所示，該幾何體是由一個直三棱柱ADE﹣BCF和一個正四棱錐P﹣ABCD組合而成，AD⊥AF，AE=AD=2．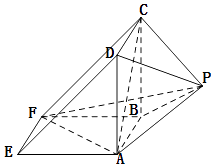 
（Ⅰ）證明：平面PAD⊥平面ABFE；
（Ⅱ）求正四棱錐P﹣ABCD的高h(yuǎn)，使得二面角C﹣AF﹣P的余弦值是 
．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)f（x）= 
是定義域在R上的奇函數(shù)，且f（2）= 
．
（1）求實數(shù)a、b的值；
（2）判斷函數(shù)f（x）的單調(diào)性，并用定義證明；
（3）解不等式：f（log 
（2x﹣2）]+f[log2（1﹣ 
x）]≥0．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù) 
為奇函數(shù)
（1）求 
的值.
（2）探究 
的單調(diào)性,并證明你的結(jié)論.
（3）求滿足 
的 
的范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知直線l：mx﹣y=1，若直線l與直線x﹣（m﹣1）y=2垂直，則m的值為 ， 動直線l：mx﹣y=1被圓C：x2﹣2x+y2﹣8=0截得的最短弦長為 ．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)函數(shù)f（x）=ex﹣x，h（x）=﹣kx3+kx2﹣x+1．
（1）求f（x）的最小值；
（2）設(shè)h（x）≤f（x）對任意x∈[0，1]恒成立時k的最大值為λ，證明：4＜λ＜6．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】函數(shù)f（x）=x2+bx+c3x（b，c∈R），若{x∈R|f（x）=0}={x∈R|f（f（x））=0}≠，則b+c的取值范圍為 ．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】若f（x）的定義域為R，f′（x）＞3恒成立，f（1）=9，則f（x）＞3x+6解集為（ ）
A.（﹣1，1）
B.（﹣1，+∞）
C.（﹣∞，﹣1）
D.（1．+∞）
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
