Question

【題目】如圖，點在以為直徑的上運動，平面，且，點分別是、的中點．

（1）求證：；

（2）若，求點平面的距離．

Answer 1

【答案】（1）見解析；（2）

【解析】

（1）證明平面可得，再結合即可得出平面，故而；（2）取中點，過作于，則可證平面，從而即為所求．

（1）證明：∵PA⊥平面ABC，BC平面ABC，

∴PA⊥BC，

∵AB是圓的直徑，∴BC⊥AC，

又AC∩PA=A，

∴BC⊥平面PAC，

又PC平面PAC．

∴BC⊥PC，

∵DE是△PBC的中位線，∴DE∥BC，

∴PC⊥DE，

∵PA=AC，D是PC的中點，

∴AD⊥PC，

又AD∩DE=D，

∴PC⊥平面ADE，又AE平面ADE，

∴PC⊥AE．

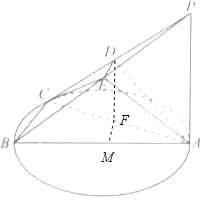
（2）解：取AC中點F，過F作FM⊥AB于M，

∵D，F分別是PC，AC的中點，

∴DF∥PA，又DF平面PAB，PA平面PAB，

∴DF∥平面PAB，

∴D到平面PAB的距離等于F到平面PAB的距離．

∵PA⊥平面ABC，FM平面ABC，

∴FM⊥PA，又FM⊥AB，PA∩AB=A，

∴FM⊥平面PAB，

∴F到平面PAB的距離為線段FM的長．

在Rt△ABC中，∵AB=2AC=2，∴AC=，

∴C到AB的距離為=，

又F為AC的中點，∴FM=．

∴點D到平面PAB的距離為．