
【題目】已知函數![]() .
.
(1)求函數![]() 的最小值;
的最小值;
(2)設![]() ,討論函數
,討論函數![]() 的單調性;
的單調性;
(3)若斜率為![]() 的直線與曲線
的直線與曲線![]() 交于
交于![]() ,
,![]() 兩點,其中
兩點,其中![]() ,求證:
,求證:![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() 時,在區間
時,在區間![]() 遞增,
遞增,![]() 時,在
時,在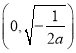 內遞增,在
內遞增,在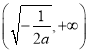 內遞減;(3)證明見解析.
內遞減;(3)證明見解析.
【解析】
試題分析:(1)借助題設條件運用導數的知識求解;(2)借助題設運用導數的知識求解;(3)依據題設先等價轉化,再構設函數運用運用導數的知識分析推證.
試題解析:
(1)![]() ,令
,令![]() ,得
,得![]() ,
,
當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,
,
則![]() 在
在![]() 內遞減,在
內遞減,在![]() 內遞增,
內遞增,
所以當![]() 時,
時,![]() .
.
(2)![]() ,
,![]() ,
,
當![]() 時,恒有
時,恒有![]() ,
,![]() 在區間
在區間![]() 內是增函數;
內是增函數;
當![]() 時,令
時,令![]() ,即
,即![]() ,解得
,解得![]() ,
,
令![]() ,即
,即![]() ,解得
,解得![]() ,
,
綜上,當![]() 時,
時,![]() 在區間
在區間![]() 內是增函數,當
內是增函數,當![]() 時,
時,![]() 在
在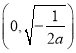 內單調遞增,在
內單調遞增,在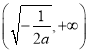 內單調遞減.
內單調遞減.
(3)證明:![]() ,要證明
,要證明![]() ,即證
,即證![]() ,
,
等價于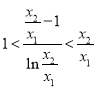 ,令
,令![]() (由
(由![]() ,知
,知![]() ),
),
則只有證![]() ,由
,由![]() ,知
,知![]() ,故等價于
,故等價于![]() (*)
(*)
<1>設![]() ,則
,則![]() ,所以
,所以![]() 在
在![]() 內是增函數,當
內是增函數,當![]() 時,
時,![]() ,所以
,所以![]() ,
,
<2>設![]() ,則
,則![]() ,所以
,所以![]() 在
在![]() 內是增函數,所以當
內是增函數,所以當![]() 時,
時,![]() ,即
,即![]() ,
,
由<1><2>知(*)成立,所以![]() .
.


 科學實驗活動冊系列答案
科學實驗活動冊系列答案科目:高中數學 來源: 題型:
【題目】設![]() :實數
:實數![]() 滿足不等式
滿足不等式![]() ,
,![]() :函數
:函數![]() 無極值點.
無極值點.
(1)若“![]() ”為假命題,“
”為假命題,“![]() ”為真命題,求實數
”為真命題,求實數![]() 的取值范圍;
的取值范圍;
(2)已知. “![]() ”為真命題,并記為
”為真命題,并記為![]() ,且
,且![]() :
:![]() ,若
,若![]() 是
是![]() 的必要不充分條件,求實數
的必要不充分條件,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校從參加高一年級期末考試的學生中抽出60名學生,將其成績(均為整數)分成六段![]() ,
, ![]() …
…![]() 后畫出如下部分頻率分布直方圖.觀察圖形的信息,回答下列問題:
后畫出如下部分頻率分布直方圖.觀察圖形的信息,回答下列問題:
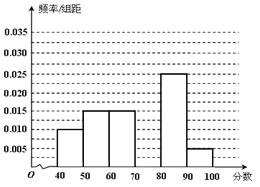
(1)求第四小組的頻率,并補全這個頻率分布直方圖;
(2)估計這次考試的及格率(60分及以上為及格)和平均分;
(3)從成績是70分以上(包括70分)的學生中選兩人,求他們在同一分數段的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了促進學生的全面發展,鄭州市某中學重視學生社團文化建設,現用分層抽樣的方法從“話劇社”,“創客社”、“演講社”三個金牌社團中抽6人組成社團管理小組,有關數據見下表(單位:人):
社團名稱 | 成員人數 | 抽取人數 |
話劇社 | 50 | a |
創客社 | 150 | b |
演講社 | 100 | c |
(1)求![]() 的值;
的值;
(2)若從“話劇社”,“創客社”,“演講社”已抽取的6人中任意抽取2人擔任管理小組組長,求這2人來自不同社團的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() 為常數,
為常數,![]() ),且數列
),且數列![]() 是首項為2,公差為2的等差數列.
是首項為2,公差為2的等差數列.
(1)若![]() ,當
,當![]() 時,求數列
時,求數列![]() 的前
的前![]() 項和
項和![]() ;
;
(2)設![]() ,如果
,如果![]() 中的每一項恒小于它后面的項,求
中的每一項恒小于它后面的項,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() :
:![]() (
(![]() )與橢圓
)與橢圓![]() :
:![]() 相交所得的弦長為
相交所得的弦長為![]()
(Ⅰ)求拋物線![]() 的標準方程;
的標準方程;
(Ⅱ)設![]() ,
,![]() 是
是![]() 上異于原點
上異于原點![]() 的兩個不同點,直線
的兩個不同點,直線![]() 和
和![]() 的傾斜角分別為
的傾斜角分別為![]() 和
和![]() ,當
,當![]() ,
,![]() 變化且
變化且![]() 為定值
為定值![]() (
(![]() )時,證明:直線
)時,證明:直線![]() 恒過定點,并求出該定點的坐標.
恒過定點,并求出該定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業生產甲乙兩種產品均需用A,B兩種原料,已知生產1噸每種產品需原料及每天原料的可用限額如右表所示,如果生產1噸甲、乙產品可獲利潤分別為3萬元、4萬元,則該企業每天可獲得最大利潤為( )
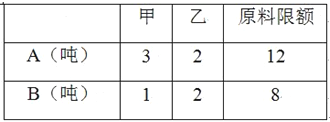
A.18萬元 B.17萬元 C.16萬元 D.12萬元
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四棱錐P-ABCD,底面ABCD是邊長為2的蓌形,PA⊥平面ABCD,PA=2,∠ABC=60°,E,F分別是BC,PC的中點。
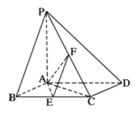
(1)求證:AE⊥PD;
(2)求二面角E-AF-C的余弦值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com