
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,其左、右焦點分別為
,其左、右焦點分別為![]() ,點
,點![]() 是坐標平面內一點,且
是坐標平面內一點,且![]() ,
, ![]() (
(![]() 為坐標原點).
為坐標原點).
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 且斜率為
且斜率為![]() 的動直線
的動直線![]() 交橢圓于
交橢圓于![]() 兩點,在
兩點,在![]() 軸上是否存在定點
軸上是否存在定點![]() ,使以
,使以![]() 為直徑的圓恒過該點?若存在,求出點
為直徑的圓恒過該點?若存在,求出點![]() 的坐標,若不存在,說明理由.
的坐標,若不存在,說明理由.
【答案】(1)![]() ;(2)點
;(2)點![]() 的坐標為
的坐標為![]() .
.
【解析】試題分析:(1)設![]() 的坐標,利用
的坐標,利用![]() 和
和![]() 求得c,通過橢圓的離心率求得a,最后利用a,b和c的關系求出b,則橢圓的方程可得.
求得c,通過橢圓的離心率求得a,最后利用a,b和c的關系求出b,則橢圓的方程可得.
(2)設出直線l的方程,與橢圓方程聯立消去y,設![]() ,
, ![]() ,則可根據韋達定理表示出
,則可根據韋達定理表示出![]() 和
和![]() ,假設在y軸上存在定點
,假設在y軸上存在定點![]() ,滿足題設,則可表示出
,滿足題設,則可表示出![]() ,利用
,利用![]() ,求出m的值
,求出m的值
試題解析:(1)設![]() ,
, ![]() ,
, ![]() ,則由
,則由![]() ,得
,得![]() ;
;
由![]() 得
得![]() ,
,
即![]() .
.
所以![]() .
.
又因為![]() ,所以
,所以![]() .
.
因此所求橢圓的方程為: ![]() .
.
(2)設動直線![]() 的方程為:
的方程為: ![]() ,
,
由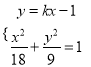 得
得![]() .
.
設![]() ,
, ![]() ,則
,則![]() ,
, ![]() .
.
假設在![]() 軸上是否存在定點
軸上是否存在定點![]() ,滿足題設,則
,滿足題設,則![]() ,
, ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
由假設得對于任意的![]() ,
, ![]() 恒成立,
恒成立,
即![]() 解得
解得![]() .
.
因此,在![]() 軸上存在定點
軸上存在定點![]() ,使以
,使以![]() 為直徑的圓恒過該點,
為直徑的圓恒過該點,
點![]() 的坐標為
的坐標為![]() .
.


 超能學典應用題題卡系列答案
超能學典應用題題卡系列答案科目:高中數學 來源: 題型:
【題目】給出以下四個問題:①x,輸出它的絕對值.②求面積為6的正方形的周長.③求三個數a,b,c中最大數.④求函數![]() 的函數值.其中不需要用條件語句來描述其算法的有 個.
的函數值.其中不需要用條件語句來描述其算法的有 個.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設等比數列{an}的各項均為正數,其前n項和為Sn , 若a1=1,a3=4.
(1)若Sk=63,求k的值;
(2)設bn=log2an , 證明數列{bn}是等差數列;
(3)設cn=(﹣1)nbn , 求T=|c1|+|c2|+|c3|+…+|cn|.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xoy中,已知橢圓C: ![]() =1(a>b>0)的離心率e=
=1(a>b>0)的離心率e= ![]() ,左頂點為A(﹣4,0),過點A作斜率為k(k≠0)的直線l交橢圓C于點D,交y軸于點E.
,左頂點為A(﹣4,0),過點A作斜率為k(k≠0)的直線l交橢圓C于點D,交y軸于點E. 
(1)求橢圓C的方程;
(2)已知P為AD的中點,是否存在定點Q,對于任意的k(k≠0)都有OP⊥EQ,若存在,求出點Q的坐標;若不存在說明理由;
(3)若過O點作直線l的平行線交橢圓C于點M,求 ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為備戰某次運動會,某市體育局組建了一個由4個男運動員和2個女運動員組成的6人代表隊并進行備戰訓練.
(1)經過備戰訓練,從6人中隨機選出2人進行成果檢驗,求選出的2人中至少有1個女運動員的概率;
(2)檢驗結束后,甲、乙兩名運動員的成績如下:
甲:70,68,74,71,72
乙:70,69,70,74,72
根據兩組數據完成圖示的莖葉圖,并通過計算說明哪位運動員的成績更穩定.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】△ABC中A(3,﹣1),AB邊上的中線CM所在直線方程為6x+10y﹣59=0,∠B的平分線方程BT為x﹣4y+10=0.
(1)求頂點B的坐標;
(2)求直線BC的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】上面圖給出的是計算1+2+4+…+22017的值的一個程序框圖,則其中判斷框內應填入的是( ) 
A.i=2017?
B.i≥2017?
C.i≥2018?
D.i≤2018?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com