Question

【題目】某校高一（1）（2）兩個班聯合開展“詩詞大會進校園，國學經典潤心田”古詩詞競賽主題班會活動，主持人從這兩個班分別隨機選出20名同學進行當場測試，他們的測試成績按[40，50），[50，60），[60，70），[70，80），[80，90），[90，100）分組，分別用頻率分布直方圖與莖葉圖統計如圖（單位：分）：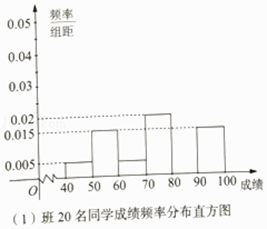
高一（2）班20名學生成績莖葉圖：

4	5
5	2
6	4 5 6 8
7	0 5 5 8 8 8 8 9
8	0 0 5 5
9	4 5

（Ⅰ）分別計算兩個班這20名同學的測試成績在[80，90）的頻率，并補全頻率分布直方圖；
（Ⅱ）分別從兩個班隨機選取1人，設這兩人中成績在[80，90）的人數為X，求X的分布列（頻率當作概率使用）．
（Ⅲ）運用所學統計知識分析比較兩個班學生的古詩詞水平．

Answer 1

【答案】解：（I）（1）班的同學成績在[80，90）的頻率為：1﹣（0.005+0.015+0.005+0.02+0.015）×10=0.4， 高一（2）班的同學成績在[80，90）的頻率為： =0.2．
補全頻率分布直方圖如下：

（II）（1）班成績在[80，90）上的人數有20×0.4=8人，（2）班成績在[80，90）上的人數有4人，
∴X的可能取值為0，1，2．
P（X=0）= = ，
P（X=1）= = ，
P（X=2）= = ．
∴X的分布列為：

X	0	1	2
P

（III）由頻率分布直方圖看，（1）班的主要成績集中在[70，100）上，
從莖葉圖看，（2）班的主要成績集中在（60，80）上，
故（1）班的古詩詞水平好于（2）班的古詩詞水平
【解析】（I）根據面積之和等于1計算（1）班成績在[80，90）的頻率；直角根據公式計算（2）班成績在[80，90）的頻率；（II）利用組合數公式計算概率；（III）根據數據的集中程度得出結論．
【考點精析】本題主要考查了頻率分布直方圖和離散型隨機變量及其分布列的相關知識點，需要掌握頻率分布表和頻率分布直方圖，是對相同數據的兩種不同表達方式.用緊湊的表格改變數據的排列方式和構成形式，可展示數據的分布情況.通過作圖既可以從數據中提取信息，又可以利用圖形傳遞信息；在射擊、產品檢驗等例子中，對于隨機變量X可能取的值，我們可以按一定次序一一列出，這樣的隨機變量叫做離散型隨機變量．離散型隨機變量的分布列：一般的,設離散型隨機變量X可能取的值為x1,x2,.....,xi,......,xn，X取每一個值 xi(i=1,2,......）的概率P(ξ=xi）＝Pi，則稱表為離散型隨機變量X 的概率分布，簡稱分布列才能正確解答此題．