【題目】已知函數
，
.
(1)討論函數
的單調性；
(2)當
時，設
，
，滿足
恒成立，求
的取值范圍.
【答案】（1）見解析；（2）
【解析】分析：（1）討論a的符號，判斷
的符號，從而得出f（x）的單調區間；
（2）令m（x）=g（x）﹣h（x），討論a的范圍，判斷
的符號，得出結論．
詳解：(1)因為
,所以定義域為
.
所以
①當
時， 
恒成立，所以
在
上單調遞增。
②當
時，令
，則
，
當
，
，所以在
上單調遞增，
當
，
，所以在
上單調遞減，
綜上所述:當時， 恒成立， 所以在上單調遞增.
當，，所以在上單調遞增，
當，，所以在上單調遞減，
(2) 
令
， 
令
，
(1)若，
，
在
遞增，
在遞增，
從而
，不符合題意.
(2)若
，當
，，在
遞增，
從而
，以下論證同(1)一樣，所以不符合題意.
(3)若
，
在恒成立，
在遞減，
，
從而在遞減
,
,
綜上所述, 
的取值范圍是.
科目：高中數學 來源： 題型：
【題目】某中學有初中學生1800人，高中學生1200人.為了解全校學生本學期開學以來的課外閱讀時間，學校采用分層抽樣方法，從中抽取了100名學生進行問卷調查.將樣本中的“初中學生”和“高中學生”，按學生的課外閱讀時間(單位：小時)各分為5組：
，
，
，
，
，得其頻率分布直方圖如圖所示.
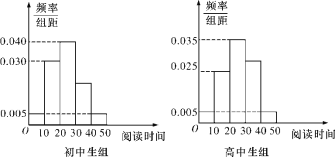
（1）估計全校學生中課外閱讀時間在小時內的總人數約是多少；
（2）從全校課外閱讀時間不足10個小時的樣本學生中隨機抽取3人，求至少有2個初中生的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】高一年級6個班級去蘇州、黃山、廈門三個地方修學旅行，每個城市至少有一個班前去，其中1班和2班不能去同一個地方，則共有_________種不同分配方法？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】據不完全統計，某廠的生產原料耗費
（單位：百萬元）與銷售額
（單位：百萬元）如下：
| 2 | 4 | 6 | 8 |
| 30 | 40 | 50 | 70 |
變量、為線性相關關系.
（1）求線性回歸方程必過的點；
（2）求線性回歸方程；
（3）若實際銷售額要求不少于
百萬元，則原材料耗費至少要多少百萬元。
，
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
.
（1）若函數
在
處的切線方程為
，求實數
，
的值；
（2）若函數在
和
兩處取得極值，求實數的取值范圍；
（3）在（2）的條件下，若
，求實數的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某地新建一家服裝廠，從今年7月份開始投產，并且前4個月的產量分別為
萬件、
萬件、
萬件、
萬件.由于產品質量好，服裝款式新穎，因此前幾個月的產品銷售情況良好.為了推銷員在推銷產品時接收訂單不產生過多或過少的情況，需要估測以后幾個月的產量，假如你是廠長，就月份x、產量y給出四種函數模型：
，
，
，
.你將利用零一種模型去估算以后幾個月的產量？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）＝logax，g（x）＝m2x2﹣2mx+1，若b＞a＞1，且f（b）
，ab＝ba．
（1）求a與b的值；
（2）當x∈[0，1]時，函數g（x）的圖象與h（x）＝f（x+1）+m的圖象僅有一個交點，求正實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知曲線
的參數方程為
(
為參數)，以原點
為極點，以
軸的非負半軸為極軸建立極坐標系，曲線
的極坐標方程為
．
（1）求曲線的極坐標方程和曲線的直角坐標方程；
（2）射線
與曲線交點為、
兩點，射線
與曲線交于點
，求
的最大值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
