
【題目】將三顆骰子各擲一次,記事件A=“三個點數都不同”,B=“至少出現一個6點”,則條件概率P(A|B),P(B|A)分別是( )
A.![]() ,
, ![]()
B.![]() ,
, ![]()
C.![]() ,
, ![]()
D.![]() ,
, ![]()
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右兩個焦點分別為
的左、右兩個焦點分別為![]() ,離心率
,離心率![]() ,短軸長為2.
,短軸長為2.
(Ⅰ)求橢圓的方程;
(Ⅱ)設點![]() 為橢圓上的一動點(非長軸端點),
為橢圓上的一動點(非長軸端點),![]() 的延長線與橢圓交于
的延長線與橢圓交于![]() 點,
點,![]() 的延長線與橢圓交于
的延長線與橢圓交于![]() 點,若
點,若![]() 面積為
面積為![]() ,求直線
,求直線![]() 的方程.
的方程.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() 或
或![]()
【解析】試題分析:(Ⅰ)由題意得![]() ,再由
,再由![]()
![]() 橢圓的方程為
橢圓的方程為![]() ;(Ⅱ)①當直線
;(Ⅱ)①當直線![]() 斜率不存在時,不妨取
斜率不存在時,不妨取![]() 面積為
面積為![]()
![]() ,不符合題意. ②當直線
,不符合題意. ②當直線![]() 斜率存在時,設直線
斜率存在時,設直線![]() , 由
, 由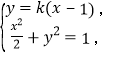
![]() 得
得![]()
![]()
![]()
![]() ,再求點
,再求點![]() 的直線
的直線![]() 的距離
的距離![]()
![]() 點
點![]() 到直線
到直線![]() 的距離為
的距離為![]() 面積為
面積為![]()
![]()
![]()
![]() ∴
∴![]() 或
或![]()
![]() 所求方程為
所求方程為![]() 或
或![]() .
.
試題解析: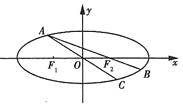
(Ⅰ)由題意得![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴橢圓的方程為![]() .
.
(Ⅱ)①當直線![]() 斜率不存在時,不妨取
斜率不存在時,不妨取![]() ,
,
∴![]() 面積為
面積為![]()
![]() ,不符合題意.
,不符合題意.
②當直線![]() 斜率存在時,設直線
斜率存在時,設直線![]() ,
,
由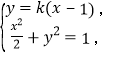 化簡得
化簡得![]() ,
,
設![]() ,
,
∴![]()
![]() ,
,
∵點![]() 的直線
的直線![]() 的距離
的距離![]() ,
,
又![]() 是線段
是線段![]() 的中點,∴點
的中點,∴點![]() 到直線
到直線![]() 的距離為
的距離為![]() ,
,
∴![]() 面積為
面積為![]()
![]()
![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() 或
或![]() ,
,
∴直線![]() 的方程為
的方程為![]() 或
或![]() .
.
【題型】解答題
【結束】
25
【題目】已知函數![]() .
.
(Ⅰ)求函數![]() 的單調區間與極值;
的單調區間與極值;
(Ⅱ)若![]() ,且
,且![]() ,證明:
,證明: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的方程為
的方程為![]() ,則其長軸長為__________;若
,則其長軸長為__________;若![]() 為
為![]() 的右焦點,
的右焦點, ![]() 為
為![]() 的上頂點,
的上頂點, ![]() 為
為![]() 上位于第一象限內的動點,則四邊形
上位于第一象限內的動點,則四邊形![]() 的面積的最大值為__________.
的面積的最大值為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】當|a|≤1,|x|≤1時,關于x的不等式|x2﹣ax﹣a2|≤m恒成立,則實數m的取值范圍是( )
A.[ ![]() ,+∞)
,+∞)
B.[ ![]() ,+∞)
,+∞)
C.[ ![]() ,+∞)
,+∞)
D.[ ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某家庭進行理財投資,根據長期收益率市場預測,投資債券等穩健型產品的一年收益與投資額成正比,其關系如圖(1);投資股票等風險型產品的一年收益與投資額的算術平方根成正比,其關系如圖(2).(注:收益與投資額單位:萬元)
(1)分別寫出兩種產品的一年收益與投資額的函數關系;
(2)該家庭現有20萬元資金,全部用于理財投資,問:怎么分配資金能使一年的投資獲得最大收益,其最大收益是多少萬元?

查看答案和解析>>
科目:高中數學 來源: 題型:
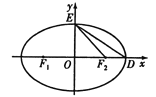
【題目】如圖![]() 為橢圓C:
為橢圓C:![]()
![]() 的左、右焦點,D,E是橢圓的兩個頂點,橢圓的離心率
的左、右焦點,D,E是橢圓的兩個頂點,橢圓的離心率![]() ,
,![]() 的面積為
的面積為![]() .若點
.若點![]() 在橢圓C上,則點
在橢圓C上,則點![]() 稱為點M的一個“橢圓”,直線
稱為點M的一個“橢圓”,直線![]() 與橢圓交于A,B兩點,A,B兩點的“橢圓”分別為P,Q.
與橢圓交于A,B兩點,A,B兩點的“橢圓”分別為P,Q.
(1)求橢圓C的標準方程;
(2)問是否存在過左焦點![]() 的直線
的直線![]() ,使得以PQ為直徑的圓經過坐標原點?若存在,求出該直線的方程;若不存在,請說明理由.
,使得以PQ為直徑的圓經過坐標原點?若存在,求出該直線的方程;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com