
【題目】已知函數![]() .
.
(1)當![]() 時,求
時,求![]() 的單調區間;
的單調區間;
(2)若對![]() ,都有
,都有![]() 成立,求
成立,求![]() 的取值范圍;
的取值范圍;
(3)當![]() 時,求
時,求![]() 在
在![]() 上的最大值.
上的最大值.
【答案】(1)![]() (2)
(2)![]() (3)
(3) ![]()
【解析】試題分析:(1)將a=1代入求出函數的表達式,通過求導令導函數大于0,從而求出函數的單調遞增區間;(2)問題轉化為![]() 對1≤x≤e恒成立.記h(x)=
對1≤x≤e恒成立.記h(x)=![]() ,通過求導得到h(x)的單調性,從而求出a的范圍;(3)先求出函數的導數,通過討論當0<x<ln2k時,當ln2k<x<k時的情況,從而得到函數f(x)的最大值.
,通過求導得到h(x)的單調性,從而求出a的范圍;(3)先求出函數的導數,通過討論當0<x<ln2k時,當ln2k<x<k時的情況,從而得到函數f(x)的最大值.
試題解析:
⑴![]() 時,
時, ![]() ,
, ![]() ,令
,令![]() ,得
,得![]() ,解得
,解得![]() .
.
所以函數![]() 的單調增區間為
的單調增區間為![]() .
.
⑵由題意 ![]() 對
對![]() 恒成立,因為
恒成立,因為![]() 時,
時, ![]() , 所以
, 所以![]() 對
對![]() 恒成立.記
恒成立.記![]() ,因為
,因為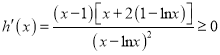 對
對![]() 恒成立,當且僅當
恒成立,當且僅當![]() 時
時![]() ,所以
,所以![]() 在
在![]() 上是增函數,
上是增函數,
所以![]() ,因此
,因此![]() .
.
⑶ 因為![]() ,由
,由![]() ,得
,得![]() 或
或![]() (舍).
(舍).
可證![]() 對任意
對任意![]() 恒成立,所以
恒成立,所以![]() ,
,
因為![]() ,所以
,所以![]() ,由于等號不能同時成立,所以
,由于等號不能同時成立,所以![]() ,于是
,于是![]() .
.
當![]() 時,
時, ![]() ,
, ![]() 在
在![]() 上是單調減函數;
上是單調減函數;
當![]() 時,
時, ![]() ,
, ![]() 在
在![]() 上是單調增函數.
上是單調增函數.
所以![]() ,
,
記![]() ,
, ![]() ,以下證明當
,以下證明當![]() 時,
時, ![]() .
.
![]() ,記
,記![]() ,
, ![]() 對
對![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上單調減函數,
上單調減函數, ![]() ,
, ![]() ,所以
,所以![]() ,使
,使![]() ,
,
當![]() 時,
時, ![]() ,
, ![]() 在
在![]() 上是單調增函數;當
上是單調增函數;當![]() 時,
時, ![]() ,
, ![]() 在
在![]() 上是單調減函數.又
上是單調減函數.又![]() ,所以
,所以![]() 對
對![]() 恒成立,
恒成立,
即![]() 對
對![]() 恒成立,所以
恒成立,所以![]() .
.


 世紀百通主體課堂小學課時同步達標系列答案
世紀百通主體課堂小學課時同步達標系列答案 世紀百通優練測系列答案
世紀百通優練測系列答案 百分學生作業本題練王系列答案
百分學生作業本題練王系列答案科目:高中數學 來源: 題型:
【題目】某工廠在政府的幫扶下,準備轉型生產一種特殊機器,生產需要投入固定成本![]() 萬元,生產與銷售均已百臺計數,且每生產
萬元,生產與銷售均已百臺計數,且每生產![]() 臺,還需增加可變成本
臺,還需增加可變成本![]() 萬元,若市場對該產品的年需求量為
萬元,若市場對該產品的年需求量為![]() 臺,每生產
臺,每生產![]() 百臺的實際銷售收入近似滿足函數
百臺的實際銷售收入近似滿足函數![]() .
.
(![]() )試寫出第一年的銷售利潤
)試寫出第一年的銷售利潤![]() (萬元)關于年產量
(萬元)關于年產量![]() (單位:百臺,
(單位:百臺,![]() ,
,![]() )的函數關系式:(說明:銷售利潤=實際銷售收入-成本)
)的函數關系式:(說明:銷售利潤=實際銷售收入-成本)
(![]() )因技術等原因,第一年的年生產量不能超過
)因技術等原因,第一年的年生產量不能超過![]() 臺,若第一年的年支出費用
臺,若第一年的年支出費用![]() (萬元)與年產量
(萬元)與年產量![]() (百臺)的關系滿足
(百臺)的關系滿足![]() ,問年產量
,問年產量![]() 為多少百臺時,工廠所得純利潤最大?
為多少百臺時,工廠所得純利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知:集合![]() ,其中
,其中
![]() .
.![]() ,稱
,稱![]() 為
為![]() 的第
的第![]() 個坐標分量.若
個坐標分量.若![]() ,且滿足如下兩條性質:
,且滿足如下兩條性質:
①![]() 中元素個數不少于
中元素個數不少于![]() 個.
個.
②![]() ,
,![]() ,
,![]() ,存在
,存在![]() ,使得
,使得![]() ,
,![]() ,
,![]() 的第
的第![]() 個坐標分量都是
個坐標分量都是![]() .則稱
.則稱![]() 為
為![]() 的一個好子集.
的一個好子集.
(![]() )若
)若![]() 為
為![]() 的一個好子集,且
的一個好子集,且![]() ,
,![]() ,寫出
,寫出![]() ,
,![]() .
.
(![]() )若
)若![]() 為
為![]() 的一個好子集,求證:
的一個好子集,求證:![]() 中元素個數不超過
中元素個數不超過![]() .
.
(![]() )若
)若![]() 為
為![]() 的一個好子集且
的一個好子集且![]() 中恰好有
中恰好有![]() 個元素,求證:一定存在唯一一個
個元素,求證:一定存在唯一一個![]() ,使得
,使得![]() 中所有元素的第
中所有元素的第![]() 個坐標分量都是
個坐標分量都是![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地方政府要將一塊如圖所示的直角梯形ABCD空地改建為健身娛樂廣場.已知AD//BC, ![]() 百米,
百米, ![]() 百米,廣場入口P在AB上,且
百米,廣場入口P在AB上,且![]() ,根據規劃,過點P鋪設兩條相互垂直的筆直小路PM,PN(小路的寬度不計),點M,N分別在邊AD,BC上(包含端點),
,根據規劃,過點P鋪設兩條相互垂直的筆直小路PM,PN(小路的寬度不計),點M,N分別在邊AD,BC上(包含端點),![]() 區域擬建為跳舞健身廣場,
區域擬建為跳舞健身廣場, ![]() 區域擬建為兒童樂園,其它區域鋪設綠化草坪,設
區域擬建為兒童樂園,其它區域鋪設綠化草坪,設![]() .
.
(1)求綠化草坪面積的最大值;
(2)現擬將兩條小路PNM,PN進行不同風格的美化,PM小路的美化費用為每百米1萬元,PN小路的美化費用為每百米2萬元,試確定M,N的位置,使得小路PM,PN的美化總費用最低,并求出最小費用.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠生產的產品![]() 的直徑均位于區間
的直徑均位于區間![]() 內(單位:
內(單位: ![]() ).若生產一件產品
).若生產一件產品![]() 的直徑位于區間
的直徑位于區間![]() 內該廠可獲利分別為10,30,20,10(單位:元),現從該廠生產的產品
內該廠可獲利分別為10,30,20,10(單位:元),現從該廠生產的產品![]() 中隨機抽取200件測量它們的直徑,得到如圖所示的頻率分布直方圖.
中隨機抽取200件測量它們的直徑,得到如圖所示的頻率分布直方圖.
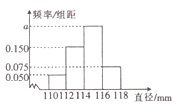
(1)求![]() 的值,并估計該廠生產一件
的值,并估計該廠生產一件![]() 產品的平均利潤;
產品的平均利潤;
(2)現用分層抽樣法從直徑位于區間![]() 內的產品中隨機抽取一個容量為5的樣本,從樣本中隨機抽取兩件產品進行檢測,求兩件產品中至多有一件產品的直徑位于區間
內的產品中隨機抽取一個容量為5的樣本,從樣本中隨機抽取兩件產品進行檢測,求兩件產品中至多有一件產品的直徑位于區間![]() 內的槪率.
內的槪率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐P﹣ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分別為AB,AC中點.
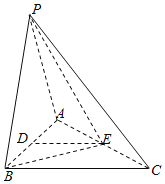
(1)求證:DE∥平面PBC;
(2)求證:AB⊥PE;
(3)求三棱錐P﹣BEC的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某校參加高二年級學業水平考試模擬考試的學生中抽取60名學生,將其數學成績分成6段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]后,畫出如圖的頻率分布直方圖.根據圖形信息,解答下列問題:
(1)估計這次考試成績的眾數,中位數,平均數;
(2)估計這次考試成績的及格率(60分及其以上為及格).

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com