
【題目】若定義在![]() 上的函數
上的函數![]() ,其圖象是連續不斷的,且存在常數
,其圖象是連續不斷的,且存在常數![]() 使得
使得![]() 對任意的實數
對任意的實數![]() 都成立,則稱
都成立,則稱![]() 是一個“
是一個“![]() 特征函數”則下列結論中正確的個數為( ).
特征函數”則下列結論中正確的個數為( ).
①![]() 是常數函數中唯一的“
是常數函數中唯一的“![]() 特征函數”;
特征函數”;
②![]() 不是“
不是“![]() 特征函數”;
特征函數”;
③“![]() 特征函數”至少有一個零點;
特征函數”至少有一個零點;
④![]() 是一個“
是一個“![]() 特征函數”;.
特征函數”;.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】分析:利用新定義“![]() 特征函數”,逐個判斷即可得到答案.
特征函數”,逐個判斷即可得到答案.
詳解:對于①設![]() 是一個“
是一個“![]() 特征函數”,則
特征函數”,則![]() ,當
,當![]() 時,可以取實數集,因此
時,可以取實數集,因此![]() 不是唯一一個常數“
不是唯一一個常數“![]() 特征函數”,故①錯誤;
特征函數”,故①錯誤;
對于②,∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
∴當![]() 時,
時,![]() ;
;![]() 時,
時,![]() 有唯一解,
有唯一解,
∴不存在常數![]() 使得
使得![]() 對任意實數
對任意實數![]() 都成立,
都成立,
∴![]() 不是“
不是“![]() 特征函數”,故②正確;
特征函數”,故②正確;
對于③,令![]() 得
得![]() ,所以
,所以![]() ,
,
若![]() ,顯然
,顯然![]() 有實數根;若
有實數根;若![]() ,
,![]() .
.
又∵![]() 的函數圖象是連續不斷的,∴
的函數圖象是連續不斷的,∴![]() 在
在![]() 上必有實數根,
上必有實數根,
因此任意的“![]() 特征函數”必有根,即任意“
特征函數”必有根,即任意“![]() 特征函數”至少有一個零點,故③正確;
特征函數”至少有一個零點,故③正確;
對于④,假設![]() 是一個“
是一個“![]() 特征函數”,則
特征函數”,則![]() 對任意實數
對任意實數![]() 成立,則有
成立,則有![]() ,而此式有解,所以
,而此式有解,所以![]() 是“
是“![]() 特征函數”,故④正確.
特征函數”,故④正確.
綜上所述,結論正確的是②③④,共![]() 個.
個.
故選![]() .
.


 名師點撥卷系列答案
名師點撥卷系列答案科目:高中數學 來源: 題型:
【題目】某工廠在政府的幫扶下,準備轉型生產一種特殊機器,生產需要投入固定成本![]() 萬元,生產與銷售均已百臺計數,且每生產
萬元,生產與銷售均已百臺計數,且每生產![]() 臺,還需增加可變成本
臺,還需增加可變成本![]() 萬元,若市場對該產品的年需求量為
萬元,若市場對該產品的年需求量為![]() 臺,每生產
臺,每生產![]() 百臺的實際銷售收入近似滿足函數
百臺的實際銷售收入近似滿足函數![]() .
.
(![]() )試寫出第一年的銷售利潤
)試寫出第一年的銷售利潤![]() (萬元)關于年產量
(萬元)關于年產量![]() (單位:百臺,
(單位:百臺,![]() ,
,![]() )的函數關系式:(說明:銷售利潤=實際銷售收入-成本)
)的函數關系式:(說明:銷售利潤=實際銷售收入-成本)
(![]() )因技術等原因,第一年的年生產量不能超過
)因技術等原因,第一年的年生產量不能超過![]() 臺,若第一年的年支出費用
臺,若第一年的年支出費用![]() (萬元)與年產量
(萬元)與年產量![]() (百臺)的關系滿足
(百臺)的關系滿足![]() ,問年產量
,問年產量![]() 為多少百臺時,工廠所得純利潤最大?
為多少百臺時,工廠所得純利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某興趣小組欲研究晝夜溫差大小與患感冒人數多少之間的關系,他們分別到氣象局與某醫院抄錄了![]() 至
至![]() 月份每月
月份每月![]() 號的晝夜溫差情況與因患感冒而就診的人數,得到如下資料:
號的晝夜溫差情況與因患感冒而就診的人數,得到如下資料:
日期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
晝夜溫差
|
|
|
|
|
|
|
就診人數 |
|
|
|
|
|
|
該興趣小組確定的研究方案是:先從這六組數據中選取![]() 組,用剩下的
組,用剩下的![]() 組數據求線性回歸方程,再用被選取的
組數據求線性回歸方程,再用被選取的![]() 組數據進行檢驗.
組數據進行檢驗.
(1)求選取的![]() 組數據恰好是相鄰兩月的概率;
組數據恰好是相鄰兩月的概率;
(2)若選取的是1月與![]() 月的兩組數據,請根據2至5月份的數據,求出
月的兩組數據,請根據2至5月份的數據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(3)若由線性回歸方程得到的估計數據與所選出的檢驗數據的誤差均不超過![]() 人,則認為得到的線性回歸方程是理想的,試問該小組所得線性回歸方程是否理想?
人,則認為得到的線性回歸方程是理想的,試問該小組所得線性回歸方程是否理想?
參考數據![]() ,
,![]()
(參考公式:
 ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知:集合![]() ,其中
,其中
![]() .
.![]() ,稱
,稱![]() 為
為![]() 的第
的第![]() 個坐標分量.若
個坐標分量.若![]() ,且滿足如下兩條性質:
,且滿足如下兩條性質:
①![]() 中元素個數不少于
中元素個數不少于![]() 個.
個.
②![]() ,
,![]() ,
,![]() ,存在
,存在![]() ,使得
,使得![]() ,
,![]() ,
,![]() 的第
的第![]() 個坐標分量都是
個坐標分量都是![]() .則稱
.則稱![]() 為
為![]() 的一個好子集.
的一個好子集.
(![]() )若
)若![]() 為
為![]() 的一個好子集,且
的一個好子集,且![]() ,
,![]() ,寫出
,寫出![]() ,
,![]() .
.
(![]() )若
)若![]() 為
為![]() 的一個好子集,求證:
的一個好子集,求證:![]() 中元素個數不超過
中元素個數不超過![]() .
.
(![]() )若
)若![]() 為
為![]() 的一個好子集且
的一個好子集且![]() 中恰好有
中恰好有![]() 個元素,求證:一定存在唯一一個
個元素,求證:一定存在唯一一個![]() ,使得
,使得![]() 中所有元素的第
中所有元素的第![]() 個坐標分量都是
個坐標分量都是![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
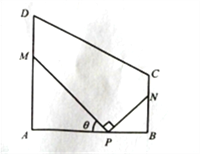
【題目】某地方政府要將一塊如圖所示的直角梯形ABCD空地改建為健身娛樂廣場.已知AD//BC, ![]() 百米,
百米, ![]() 百米,廣場入口P在AB上,且
百米,廣場入口P在AB上,且![]() ,根據規劃,過點P鋪設兩條相互垂直的筆直小路PM,PN(小路的寬度不計),點M,N分別在邊AD,BC上(包含端點),
,根據規劃,過點P鋪設兩條相互垂直的筆直小路PM,PN(小路的寬度不計),點M,N分別在邊AD,BC上(包含端點),![]() 區域擬建為跳舞健身廣場,
區域擬建為跳舞健身廣場, ![]() 區域擬建為兒童樂園,其它區域鋪設綠化草坪,設
區域擬建為兒童樂園,其它區域鋪設綠化草坪,設![]() .
.
(1)求綠化草坪面積的最大值;
(2)現擬將兩條小路PNM,PN進行不同風格的美化,PM小路的美化費用為每百米1萬元,PN小路的美化費用為每百米2萬元,試確定M,N的位置,使得小路PM,PN的美化總費用最低,并求出最小費用.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐P﹣ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分別為AB,AC中點.
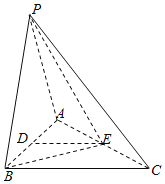
(1)求證:DE∥平面PBC;
(2)求證:AB⊥PE;
(3)求三棱錐P﹣BEC的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】網購已經成為一種時尚,商家為了鼓勵消費,購買時在店鋪領取優惠券,買后給予好評返還現金等促銷手段.經統計,近五年某店鋪用于促銷的費用![]() (萬元)與當年度該店鋪的銷售收人
(萬元)與當年度該店鋪的銷售收人![]() (萬元)的數據如下表:
(萬元)的數據如下表:
年份 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 |
促銷費用 |
|
|
|
|
|
銷售收入 |
|
|
|
|
|
(1)請根據上表提供的數據,用最小二乘法求出/span>![]() 關于
關于![]() 的線性回歸方
的線性回歸方![]() ;
;
(2)2018年度該店鋪預測銷售收人至少達到![]() 萬元,則該店鋪至少準備投入多少萬元的促銷費?
萬元,則該店鋪至少準備投入多少萬元的促銷費?
參考公式: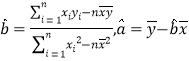
參考數據: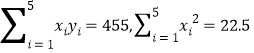
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com