
���}Ŀ���x��4-4������(bi��o)ϵ�c����(sh��)����
��ƽ��ֱ������(bi��o)ϵ![]() �У�ֱ��
�У�ֱ��![]() �ą���(sh��)���̞�
�ą���(sh��)���̞�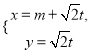 ��
��![]() �酢��(sh��)����������(bi��o)ԭ�c(di��n)��O�c(di��n)��
�酢��(sh��)����������(bi��o)ԭ�c(di��n)��O�c(di��n)�� ![]() �S�������S��O�S�����O����(bi��o)ϵ������
�S�������S��O�S�����O����(bi��o)ϵ������![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() ����ֱ��
����ֱ��![]() ��(j��ng)�^����
��(j��ng)�^����![]() �����c(di��n)
�����c(di��n)![]() ��
��
��1����![]() ��ֵ��ֱ��
��ֵ��ֱ��![]() ����ͨ���̣�
����ͨ���̣�
��2���O(sh��)����![]() �ă�(n��i)�Ӿ��ε����L��
�ă�(n��i)�Ӿ��ε����L��![]() ����
����![]() �����ֵ��
�����ֵ��
���𰸡���1��Ҋ��������2��![]() ��
��
��������ԇ�}��������1����![]() ��
�� ![]() ������ʽ��������
������ʽ��������![]() ������
������![]() ����ֱ��
����ֱ��![]() ����ͨ���̞�
����ͨ���̞�![]() �������c(di��n)����õ�
�������c(di��n)����õ�![]() ������ֱ��
������ֱ��![]() ����ͨ���̞�
����ͨ���̞�![]() ����2���O(sh��)�E�A
����2���O(sh��)�E�A![]() �ă�(n��i)�Ӿ����ڵ�һ������c(di��n)��
�ă�(n��i)�Ӿ����ڵ�һ������c(di��n)��![]() �����ԙE�A
�����ԙE�A![]() �ă�(n��i)�Ӿ��ε����L��
�ă�(n��i)�Ӿ��ε����L��![]() ������
������![]() �����˕r(sh��)�E�A
�����˕r(sh��)�E�A![]() �ă�(n��i)�Ӿ��ε����Lȡ�����ֵ
�ă�(n��i)�Ӿ��ε����Lȡ�����ֵ![]() ��
��
ԇ�}������
��1����?y��n)�����![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() ����
����![]() ����
����![]() ��
�� ![]() ������ʽ��������
������ʽ��������![]() ����������
����������![]() ��ֱ������(bi��o)���̞�
��ֱ������(bi��o)���̞�![]() ������
������![]() ��
�� ![]() ��
��
ֱ��![]() ����ͨ���̞�
����ͨ���̞�![]() ����
����![]() ����ֱ�����̵�
����ֱ�����̵�![]() ������ֱ��
������ֱ��![]() ����ͨ���̞�
����ͨ���̞�![]() ����
����
��2���O(sh��)�E�A![]() �ă�(n��i)�Ӿ����ڵ�һ������c(di��n)��
�ă�(n��i)�Ӿ����ڵ�һ������c(di��n)��![]() ��
��![]() �������ԙE�A
�������ԙE�A![]() �ă�(n��i)�Ӿ��ε����L��
�ă�(n��i)�Ӿ��ε����L��![]() ������
������![]() �����˕r(sh��)�E�A
�����˕r(sh��)�E�A![]() �ă�(n��i)�Ӿ��ε����Lȡ�����ֵ
�ă�(n��i)�Ӿ��ε����Lȡ�����ֵ![]() ��
��



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��������һ�f����������һ�������B(y��ng)���^���ѽ�(j��ng)�������ģ������о��ԌW(xu��)��(x��)����Ҫ��ij��W(xu��)���ռ����֙C(j��)�����\(y��n)��(d��ng)���F(tu��n)�(du��)���ض��ס��҃ɂ�(g��)�༉(j��)![]() ���ɆTһ�����ߵIJ���(sh��)��Ȼ����÷ӳ�ӵķ�������
���ɆTһ�����ߵIJ���(sh��)��Ȼ����÷ӳ�ӵķ�������![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() �ӳ�ȡ��20���ɆT�IJ���(sh��)�����L���������в��������o�~�D����λ��ǧ������
�ӳ�ȡ��20���ɆT�IJ���(sh��)�����L���������в��������o�~�D����λ��ǧ������

��֪�ס��҃ɰ����߲���(sh��)��ƽ��ֵ����44ǧ��.
��1����![]() ��ֵ��
��ֵ��
��2����������![]() ����ס��҃ɂ�(g��)�༉(j��)100���ɆT�����߲���(sh��)��
����ס��҃ɂ�(g��)�༉(j��)100���ɆT�����߲���(sh��)��![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ���ӵ��˔�(sh��)��
���ӵ��˔�(sh��)��
����������Ӌ(j��)ԓ�F(tu��n)�(du��)��һ�����߲���(sh��)����40ǧ�����˔�(sh��)��̎��![]() ǧ�����˔�(sh��)��12�ˣ���
ǧ�����˔�(sh��)��12�ˣ���![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D���ڰ돽��1������AOB�У�O��ԭ�c(di��n)����![]() ���c(di��n)P��x��y����
���c(di��n)P��x��y����![]() ������һ�c(di��n)���txy+x+y�����ֵ�飨������
������һ�c(di��n)���txy+x+y�����ֵ�飨������

A. ![]() B. 1 C.
B. 1 C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���O(sh��)���}![]() ����(sh��)
����(sh��)![]() ��ֵ��?y��n)?/span>
��ֵ��?y��n)?/span>![]() �����}
�����}![]() ������ʽ
������ʽ![]() �������������}��
�������������}��![]() ���������}���ҡ�
���������}���ҡ�![]() ��������}����(sh��)��(sh��)
��������}����(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D����֪![]() ��
�� ![]() �քe��E�A
�քe��E�A![]() ��
�� ![]() ���ϡ��½��c(di��n)��
���ϡ��½��c(di��n)�� ![]() �ǒ��タ
�ǒ��タ![]() ��
�� ![]() �Ľ��c(di��n)���c(di��n)
�Ľ��c(di��n)���c(di��n)![]() ��
��![]() �c
�c![]() �ڵڶ����Ľ��c(di��n)����
�ڵڶ����Ľ��c(di��n)����![]() ��
��

��1����E�A![]() �ķ��̣�
�ķ��̣�
��2���c�A![]() ���е�ֱ��
���е�ֱ��![]() ��
�� ![]() ������
������![]() �����E�A
�����E�A![]() ���c(di��n)
���c(di��n)![]() ��
�� ![]() �����E�A
�����E�A![]() ��һ�c(di��n)
��һ�c(di��n)![]() �M��
�M��![]() ����(sh��)��(sh��)
����(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ������(sh��)![]() .
.
(1)������(sh��)![]() ���c(di��n)
���c(di��n)![]() ̎���о��cֱ��
̎���о��cֱ��![]() ƽ��,��(sh��)��(sh��)
ƽ��,��(sh��)��(sh��)![]() ��ֵ��
��ֵ��
(2)������(sh��)![]() ��
��![]() �φ��{(di��o)�f��,��(sh��)��(sh��)
�φ��{(di��o)�f��,��(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
(3)��(1)�ėl����,��![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
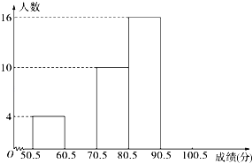
���}Ŀ�������W(xu��)���˽�h(hu��n)��֪�R(sh��)������(qi��ng)�h(hu��n)�����R(sh��)��ij�ЌW(xu��)�e����һ�����h(hu��n)��֪�R(sh��)��ِ��������900���W(xu��)���������@�θ�ِ�����˽Ȿ�θ�ِ�ɿ���r�����г�ȡ�˲��W(xu��)���ijɿ����÷־�������(sh��)���M�֞�100�֣��M(j��n)�нy(t��ng)Ӌ(j��)��Ո�����(j��)��δ��ɲ��оֲ��ۓp���l�ʷֲ������l��(sh��)�ֲ�ֱ���D��������І��}��
��1������l�ʷֲ����Ŀո���ֱ�����ڱ����(n��i)����
��2���a(b��)ȫ�l��(sh��)�ֲ�ֱ���D��
��3�����ɿ���75.5��85�ČW(xu��)������Ȫ�(ji��ng)�����@�ö��Ȫ�(ji��ng)�ČW(xu��)���s������ˣ�

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪���タ![]() �Ľ��c(di��n)��
�Ľ��c(di��n)��![]() ,�p����
,�p����![]() ���ҽ��c(di��n)��
���ҽ��c(di��n)��![]() ���^�c(di��n)
���^�c(di��n)![]() ��ֱ���c���タ�ڵ�һ���Ľ��c(di��n)��
��ֱ���c���タ�ڵ�һ���Ľ��c(di��n)��![]() ���Ғ��タ���c(di��n)
���Ғ��タ���c(di��n)![]() ̎���о��cֱ��
̎���о��cֱ��![]() ��ֱ���t
��ֱ���t![]() �����ֵ���� ��
�����ֵ���� ��
A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����һ����ݮ�У��S�C(j��)��ȡ![]() ��(g��)������������λ���ˣ����l�ʷֲ������£�
��(g��)������������λ���ˣ����l�ʷֲ������£�
�ֽM�������� |
|
|
|
|
�l��(sh��)����(g��)�� |
|
|
|
|
��֪��![]() ��(g��)��ݮ���S�C(j��)��ȡһ��(g��)���鵽������
��(g��)��ݮ���S�C(j��)��ȡһ��(g��)���鵽������![]() �IJ�ݮ�ĸ��ʞ�
�IJ�ݮ�ĸ��ʞ�![]() ��
��
��1�����![]() ��
��![]() ��ֵ��
��ֵ��
��2���÷ӳ�ӵķ�����������![]() ��
��![]() �IJ�ݮ�й���ȡ
�IJ�ݮ�й���ȡ![]() ��(g��)���ُ��@
��(g��)���ُ��@![]() ��(g��)��ݮ����ȡ
��(g��)��ݮ����ȡ![]() ��(g��)����������
��(g��)����������![]() ��
��![]() ���
�и���![]() ��(g��)�ĸ��ʣ�
��(g��)�ĸ��ʣ�
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com