
【題目】為了治理空氣污染,某市設![]() 個監測站用于監測空氣質量指數
個監測站用于監測空氣質量指數![]() ,其中在輕度污染區、中度污染區、重度污染區分別設有
,其中在輕度污染區、中度污染區、重度污染區分別設有![]() 、
、![]() 、
、![]() 個監測站,并以
個監測站,并以![]() 個監測站測得的
個監測站測得的![]() 的平均值為依據播報該市的空氣質量.
的平均值為依據播報該市的空氣質量.
(1)若某日播報的![]() 為
為![]() ,已知輕度污染區
,已知輕度污染區![]() 平均值為
平均值為![]() ,中度污染區
,中度污染區![]() 平均值為
平均值為![]() ,求重試污染區
,求重試污染區![]() 平均值;
平均值;
(2)如圖是![]() 年
年![]() 月份
月份![]() 天的
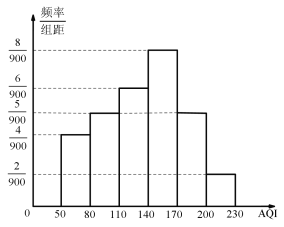
天的![]() 的頻率分布直方圖,
的頻率分布直方圖,![]() 月份僅有
月份僅有![]() 天
天![]() 在
在![]() 內.
內.
①某校參照官方公布的![]() ,如果周日
,如果周日![]() 小于
小于![]() 就組織學生參加戶外活動,以統計數據中的頻率為概率,求該校學生周日能參加戶外活動的概率;
就組織學生參加戶外活動,以統計數據中的頻率為概率,求該校學生周日能參加戶外活動的概率;
②環衛部門從![]() 月份
月份![]() 不小于
不小于![]() 的數據中抽取兩天的數據進行研究,求抽取的這兩天中
的數據中抽取兩天的數據進行研究,求抽取的這兩天中![]() 值都在
值都在![]() 的概率.
的概率.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() .
.
【解析】
(1)設重度污染區![]() 平均值為
平均值為![]() ,根據題意可得出關于
,根據題意可得出關于![]() 的方程,進而可求得
的方程,進而可求得![]() 的值;
的值;
(2)①計算出![]() 月份
月份![]() 天中
天中![]() 不小于
不小于![]() 的天數,進而可求得該校學生周日能參加戶外活動的概率;
的天數,進而可求得該校學生周日能參加戶外活動的概率;
②由題意可知,![]() 在
在![]() 上的有
上的有![]() 天,編號分別設為
天,編號分別設為![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() 在
在![]() 上的有
上的有![]() 天,編號設為
天,編號設為![]() 、
、![]() ,列出所有的基本事件,并確定事件“抽取的這兩天中
,列出所有的基本事件,并確定事件“抽取的這兩天中![]() 值都在
值都在![]() ”所包含的基本事件,利用古典概型的概率公式可求得結果.
”所包含的基本事件,利用古典概型的概率公式可求得結果.
(1)設重度污染區![]() 平均值為
平均值為![]() ,則
,則![]() ,解得
,解得![]() ;
;
(2)①![]() 在
在![]() 上的有
上的有![]() 天,
天,
![]() 在
在![]() 上的有
上的有![]() 天,
天,
![]() 在
在![]() 上的有
上的有![]() 天,
天,
所以![]() 月份
月份![]() 不小于
不小于![]() 天的共
天的共![]() 天.
天.
即能參加戶外活動的概率為![]() ;
;
②由①![]() 在
在![]() 上的有
上的有![]() 天,編號分別設為
天,編號分別設為![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,
![]() 在
在![]() 上的有
上的有![]() 天,編號設為
天,編號設為![]() 、
、![]() ,
,
從![]() 天中抽取兩天有:
天中抽取兩天有:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、
![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共
,共![]() 種.
種.
滿足條件的有![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共
,共![]() 種,
種,
所以滿足條件的概率為![]() .
.


科目:高中數學 來源: 題型:
【題目】某植物學家培養出一種觀賞性植物,會開出紅花或黃花,已知該植物第一代開紅花和黃花的概率都是![]() ,從第二代開始,若上一代開紅花,則這一代開紅花的概率是
,從第二代開始,若上一代開紅花,則這一代開紅花的概率是![]() ,開黃花的概率是
,開黃花的概率是![]() ;若上一代開黃花,則這一代開紅花的概率是
;若上一代開黃花,則這一代開紅花的概率是![]() ,開黃花的概率是
,開黃花的概率是![]() .記第n代開紅花的概率為
.記第n代開紅花的概率為![]() ,第n代開黃花的概率為
,第n代開黃花的概率為![]() .
.
(1)求![]() ;
;
(2)①證明:數列![]() 為等比數列;
為等比數列;
②第![]() 代開哪種顏色花的概率更大?
代開哪種顏色花的概率更大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 是拋物線
是拋物線![]() :
:![]() 上的一點,其焦點為點
上的一點,其焦點為點![]() ,且拋物線
,且拋物線![]() 在點
在點![]() 處的切線
處的切線![]() 交圓
交圓![]() :
:![]() 于不同的兩點
于不同的兩點![]() ,
,![]() .
.
(1)若點![]() ,求
,求![]() 的值;
的值;
(2)設點![]() 為弦
為弦![]() 的中點,焦點
的中點,焦點![]() 關于圓心
關于圓心![]() 的對稱點為
的對稱點為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某省為迎接新高考,擬先對考生某選考學科的實際得分進行等級賦分,再按賦分后的分數從高分到低分劃A、B、C、D、E五個等級,考生實際得分經賦分后的分數在到1之間.在等級賦分科學性論證時,對過去一年全省高考考生的該學科成績重新賦分后進行分析,隨機抽取2000名學生的該學科賦分后的成績,得到如下頻率分布直方圖:(不考慮缺考考生的試卷)
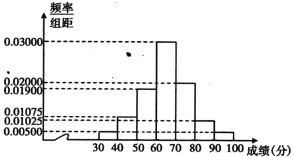
附:若X~N(μ,σ2),則P(μ-σ<X<μ+σ)=0.6826,P(μ-2σ<X<μ+2σ)=0.9544,P(μ-3σ<X<μ+3σ)=0.9974,![]() =14.59,∑(xi-
=14.59,∑(xi-![]() )2pi=213
)2pi=213
(1)求這2000名考生賦分后該學科的平均![]() (同一組中數據用該組區間中點作代表);
(同一組中數據用該組區間中點作代表);
(2)由頻率分布直方圖可以認為,學生經過賦分以后的成績X服從正態分布X~N(μ,σ2),其中μ近似為樣本平均數![]() ,σ2近似為樣本方差s2:
,σ2近似為樣本方差s2:
(i)利用正態分布,求P(50.41<X<79.59);
(ii)某市有20000名高三學生,記Y表示這20000名高三學生中賦分后該學科等級為A等(即得分大于79.59)的學生數,利用(i)的結果,求EY.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的普通方程為
的普通方程為![]() ,直線
,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),其中
為參數),其中![]() .以坐標
.以坐標![]() 為極點,以
為極點,以![]() 軸非負半軸為極軸,建立極坐標系.
軸非負半軸為極軸,建立極坐標系.
(1)求曲線![]() 的極坐標方程和直線
的極坐標方程和直線![]() 的普通方程;
的普通方程;
(2)設點![]() ,
,![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 與
與![]() 的交點分別為
的交點分別為![]() ,
,![]() .當
.當![]() 為等腰直角三角形時,求直線
為等腰直角三角形時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
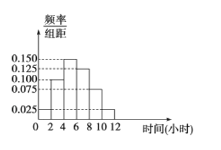
【題目】某中學共有1000人,其中男生700人,女生300人,為了了解該校學生每周平均體育鍛煉時間的情況以及經常進行體育鍛煉的學生是否與性別有關(經常進行體育鍛煉是指:周平均體育鍛煉時間不少于4小時),現在用分層抽樣的方法從中收集200位學生每周平均體育鍛煉時間的樣本數據(單位:小時),其頻率分布直方圖如圖.已知在樣本數據中,有40位女生的每周平均體育鍛煉時間超過4小時,根據獨立性檢驗原理( )
附: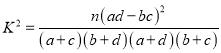 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.01 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
A.有95%的把握認為“該校學生每周平均體育鍛煉時間與性別無關”
B.有90%的把握認為“該校學生每周平均體育鍛煉時間與性別有關”
C.有90%的把握認為“該校學生每周平均體育鍛煉時間與性別無關”
D.有95%的把握認為“該校學生每周平均體育鍛煉時間與性別有關”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,點
,點![]() 在橢圓
在橢圓![]() 上.
上.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設![]() 為原點,過原點的直線(不與
為原點,過原點的直線(不與![]() 軸垂直)與橢圓
軸垂直)與橢圓![]() 交于
交于![]() 、
、![]() 兩點,直線
兩點,直線![]() 、
、![]() 與
與![]() 軸分別交于點
軸分別交于點![]() 、
、![]() .問:
.問:![]() 軸上是否存在定點
軸上是否存在定點![]() ,使得
,使得![]() ?若存在,求點
?若存在,求點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
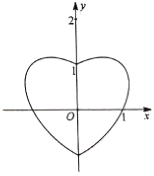
【題目】數學中有許多形狀優美、寓意美好的曲線,如下圖就是在平面直角坐標系的“心形曲線”,又名RC心形線.如果以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系,其RC心形線的極坐標方程為
軸正半軸為極軸,建立極坐標系,其RC心形線的極坐標方程為![]() .
.
(1)求RC心形線的直角坐標方程;
(2)已知![]() 與直線
與直線![]() (
(![]() 為參數),若直線
為參數),若直線![]() 與RC心形線交于兩點
與RC心形線交于兩點![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com