
【題目】在平面直角坐標系xOy中,橢圓![]() 左、右焦點分別為
左、右焦點分別為![]() ,
,![]() ,離心率為
,離心率為![]() ,兩準線間距離為8,圓O的直徑為
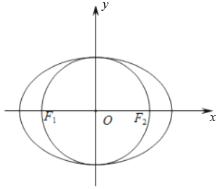
,兩準線間距離為8,圓O的直徑為![]() ,直線l與圓O相切于第四象限點T,與y軸交于M點,與橢圓C交于點N(N點在T點上方),且
,直線l與圓O相切于第四象限點T,與y軸交于M點,與橢圓C交于點N(N點在T點上方),且![]() .
.
(1)求橢圓C的標準方程;
(2)求直線l的方程;
(3)求直線l上滿足到![]() ,
,![]() 距離之和為
距離之和為![]() 的所有點的坐標.
的所有點的坐標.
【答案】(1)![]() (2)
(2)![]() .(3)
.(3)![]() 和
和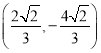 .
.
【解析】
(1) 根據橢圓的性質、離心率和兩準線間的距離,列出以下方程:![]() ①,
①,![]() ②,
②,![]() ③,然后求解即可.
③,然后求解即可.
(2) 法一:設切點![]() ,則
,則![]() ⑤, 利用
⑤, 利用![]() 和
和![]() 為核心參數,依次表示直線OT的斜率,直線
為核心參數,依次表示直線OT的斜率,直線![]() 的方程,以及N點的坐標,然后列方程求解即可求出
的方程,以及N點的坐標,然后列方程求解即可求出![]() 和
和![]() ,進而即可求解.
,進而即可求解.
法二:設![]() ,
,![]() ,然后,以
,然后,以![]() ,
,![]() ,
,![]() 為核心參數,列出直線
為核心參數,列出直線![]() 的方程,又因
的方程,又因![]() 與
與![]() 相切,則列出圓心距
相切,則列出圓心距![]() 的方程,最后根據(1)中的方程,聯合求解即可.
的方程,最后根據(1)中的方程,聯合求解即可.
(3) 因為到![]() ,
,![]() 距離之和為
距離之和為![]() 的所有點的集合為橢圓C,
的所有點的集合為橢圓C,
所以滿足題意的點為直線l與橢圓C的公共點,
聯立![]() ④和
④和![]() ⑨得:
⑨得: ,然后求解即可.
,然后求解即可.
解:(1)設橢圓C的焦距為![]() ,因為離心率為
,因為離心率為![]() ①,
①,
兩準線間距離為![]() ②,又
②,又![]() ③,
③,
由①②③解得![]() ,
,![]() .則橢圓C的標準方程為
.則橢圓C的標準方程為![]() ④
④
(2)法一:設切點![]() ,則
,則![]() ⑤,因T在第四象限,所以
⑤,因T在第四象限,所以![]() ,
,![]() ,
,
直線OT的斜率![]() ,因為
,因為![]() ,所以直線
,所以直線![]() 的斜率
的斜率![]() ,
,
直線![]() ,由⑤得:
,由⑤得:![]() ⑥,
⑥,
令![]() ,得
,得 ,
,
因為![]() ,
,![]() ,所以,T為MN中點,所以
,所以,T為MN中點,所以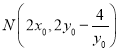 ,
,
代入(1)中④得: ,解得:
,解得:![]() ,
,![]() ,
,
代入⑥式得:直線l的方程為![]() .
.
法二:設![]() ,
,![]() ,則
,則![]() ⑤,設直線
⑤,設直線![]() ⑦,
⑦,
因為切點T在第四象限,所以![]() ,
,![]() ,
,![]() .
.
因l與![]() 相切,則圓心距
相切,則圓心距![]() ,
,![]() ⑧,
⑧,
因為![]() ,則
,則![]() ,所以
,所以![]() ⑨,
⑨,
聯立⑤⑨解得:![]() ,
,![]() ,
,
因為![]() ,所以
,所以![]() ,
,![]() ,
,
則![]() ,由⑧得
,由⑧得 ,解得
,解得![]() ,
,![]() .
.
當![]() 時,
時,![]() ,與
,與![]() 矛盾.則
矛盾.則![]() ,代入⑧,得
,代入⑧,得![]() ,
,
所以直線l方程為![]() ⑨.
⑨.
(3)因為到![]() ,
,![]() 距離之和為
距離之和為![]() 的所有點的集合為橢圓C,
的所有點的集合為橢圓C,
所以滿足題意的點為直線l與橢圓C的公共點,
聯立④⑨得: ,得
,得![]() ,即
,即 或
或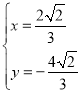 ,
,
所以滿足條件的點的坐標為![]() 和
和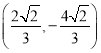 .
.


科目:高中數學 來源: 題型:
【題目】在三棱錐P﹣ABC中,平面PBC⊥平面ABC,∠ACB=90°,BC=PC=2,若AC=PB,則三棱錐P﹣ABC體積的最大值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,矩形ABCD中,![]() ,
,![]() ,
,![]() 是AD的中點,將
是AD的中點,將![]() 沿BE翻折,記為
沿BE翻折,記為![]() ,在翻折過程中,①點
,在翻折過程中,①點![]() 在平面BCDE的射影必在直線AC上;②記
在平面BCDE的射影必在直線AC上;②記![]() 和
和![]() 與平面BCDE所成的角分別為
與平面BCDE所成的角分別為![]() ,
,![]() ,則
,則![]() 的最大值為0;③設二面角
的最大值為0;③設二面角![]() 的平面角為
的平面角為![]() ,則
,則![]() .其中正確命題的個數是( )
.其中正確命題的個數是( )
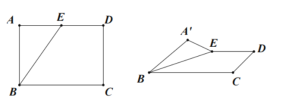
A.0B.1C.2D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是一“T”型水渠的平面視圖(俯視圖),水渠的南北方向和東西方向軸截面均為矩形,南北向渠寬為4m,東西向渠寬![]() m(從拐角處,即圖中
m(從拐角處,即圖中![]() ,
,![]() 處開始).假定渠內的水面始終保持水平位置(即無高度差).
處開始).假定渠內的水面始終保持水平位置(即無高度差).
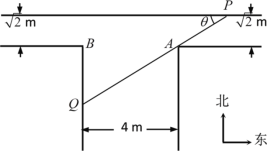
(1)在水平面內,過點![]() 的一條直線與水渠的內壁交于
的一條直線與水渠的內壁交于![]() ,
,![]() 兩點,且與水渠的一邊的夾角為
兩點,且與水渠的一邊的夾角為![]() ,將線段
,將線段![]() 的長度
的長度![]() 表示為
表示為![]() 的函數;
的函數;
(2)若從南面漂來一根長為7m的筆直的竹竿(粗細不計),竹竿始終浮于水平面內,且不發生形變,問:這根竹竿能否從拐角處一直漂向東西向的水渠(不會卡住)?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知梯形ABCD滿足AB∥CD,∠BAD=45°,以A,D為焦點的雙曲線Γ經過B,C兩點.若CD=7AB,則雙曲線Γ的離心率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某運輸公司每天至少向某地運送![]() 物質,該公司有8輛載重為
物質,該公司有8輛載重為![]() 的
的![]() 型卡車與4輛載重為
型卡車與4輛載重為![]() 的
的![]() 型卡車,有10名駕駛員,每輛卡車每天往返的次數為
型卡車,有10名駕駛員,每輛卡車每天往返的次數為![]() 型卡車4次,
型卡車4次,![]() 型卡車3次;每輛卡車每天往返的成本為
型卡車3次;每輛卡車每天往返的成本為![]() 型卡車320元,
型卡車320元,![]() 型卡車504元,你認為該公司怎樣調配車輛,使運費成本最低,最低運費是多少?
型卡車504元,你認為該公司怎樣調配車輛,使運費成本最低,最低運費是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com