
【題目】已知當x∈[0,1]時,函數y=(mx﹣1)2 的圖象與y= ![]() +m的圖象有且只有一個交點,則正實數m的取值范圍是( )
+m的圖象有且只有一個交點,則正實數m的取值范圍是( )
A.(0,1]∪[2 ![]() ,+∞)
,+∞)
B.(0,1]∪[3,+∞)
C.(0, ![]() )∪[2
)∪[2 ![]() ,+∞)
,+∞)
D.(0, ![]() ]∪[3,+∞)
]∪[3,+∞)
【答案】B
【解析】解:根據題意,由于m為正數,y=(mx﹣1)2 為二次函數,在區間(0, ![]() )為減函數,(
)為減函數,( ![]() ,+∞)為增函數,
,+∞)為增函數,
函數y= ![]() +m為增函數,
+m為增函數,
分2種情況討論:
①、當0<m≤1時,有 ![]() ≥1,
≥1,
在區間[0,1]上,y=(mx﹣1)2 為減函數,且其值域為[(m﹣1)2 , 1],
函數y= ![]() +m為增函數,其值域為[m,1+m],
+m為增函數,其值域為[m,1+m],
此時兩個函數的圖象有1個交點,符合題意;
②、當m>1時,有 ![]() <1,
<1,
y=(mx﹣1)2 在區間(0, ![]() )為減函數,(
)為減函數,( ![]() ,1)為增函數,
,1)為增函數,
函數y= ![]() +m為增函數,其值域為[m,1+m],
+m為增函數,其值域為[m,1+m],
若兩個函數的圖象有1個交點,則有(m﹣1)2≥1+m,
解可得m≤0或m≥3,
又由m為正數,則m≥3;
綜合可得:m的取值范圍是(0,1]∪[3,+∞);
故選:B.
【考點精析】關于本題考查的函數的值域和函數單調性的性質,需要了解求函數值域的方法和求函數最值的常用方法基本上是相同的.事實上,如果在函數的值域中存在一個最小(大)數,這個數就是函數的最小(大)值.因此求函數的最值與值域,其實質是相同的;函數的單調區間只能是其定義域的子區間 ,不能把單調性相同的區間和在一起寫成其并集才能得出正確答案.


科目:高中數學 來源: 題型:
【題目】為了讓觀賞游玩更便捷舒適,常州恐龍園推出了代步工具租用服務.已知有腳踏自行車![]() 與電動自行車
與電動自行車![]() 兩種車型,采用分段計費的方式租用.
兩種車型,采用分段計費的方式租用.![]() 型車每
型車每![]() 分鐘收費
分鐘收費![]() 元(不足
元(不足![]() 分鐘的部分按
分鐘的部分按![]() 分鐘計算),
分鐘計算),![]() 型車每
型車每![]() 分鐘收費
分鐘收費![]() 元(不足
元(不足![]() 分鐘的部分按
分鐘的部分按![]() 分鐘計算),現有甲乙丙丁四人,分別相互獨立地到租車點租車騎行(各租一車一次),設甲乙丙丁不超過
分鐘計算),現有甲乙丙丁四人,分別相互獨立地到租車點租車騎行(各租一車一次),設甲乙丙丁不超過![]() 分鐘還車的概率分別為
分鐘還車的概率分別為![]() ,并且四個人每人租車都不會超過
,并且四個人每人租車都不會超過![]() 分鐘,甲乙丙均租用
分鐘,甲乙丙均租用![]() 型車,丁租用
型車,丁租用![]() 型車.
型車.
(1)求甲乙丙丁四人所付的費用之和為25元的概率;
(2)求甲乙丙三人所付的費用之和等于丁所付的費用的概率;
(3)設甲乙丙丁四人所付費用之和為隨機變量![]() ,求
,求![]() 的概率分布和數學期望.
的概率分布和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】假設關于某設備使用年限x(年)和所支出的維修費用y(萬元)有如下統計資料:
i | 1 | 2 | 3 | 4 | 5 |
|
xi | 2 | 3 | 4 | 5 | 6 | |
yi | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 | |
xi yi | 4.4 | 11.4 | 22.0 | 32.5 | 42.0 |
若由資料知,y對x呈線性相關關系,試求:
(1)回歸直線方程;
(2)估計使用年限為10年時,維修費用約是多少
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若一條直線a與平面α內的一條直線b所成的角為30°,則下列說法正確的是( )
A. 直線a與平面α所成的角為30° B. 直線a與平面α所成的角大于30°
C. 直線a與平面α所成的角小于30° D. 直線a與平面α所成的角不超過30°
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以下關于線性回歸的判斷,正確的個數是( )

①若散點圖中所有點都在一條直線附近,則這條直線為回歸直線;
②散點圖中的絕大多數都線性相關,個別特殊點不影響線性回歸,如圖中的A,B,C點;
③已知直線方程為![]() =0.50x-0.81,則x=25時,y的估計值為11.69;
=0.50x-0.81,則x=25時,y的估計值為11.69;
④回歸直線方程的意義是它反映了樣本整體的變化趨勢.
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校從參加高三模擬考試的學生中隨機抽取60名學生,將其數學成績(均為整數)分成六組[90,100),[100,110),…,[140,150]后得到如下部分頻率分布直方圖,觀察圖形的信息,回答下列問題:
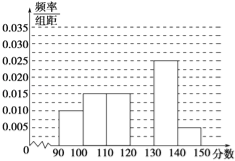
(1)求分數在[120,130)內的頻率;
(2)若在同一組數據中,將該組區間的中點值(如:組區間[100,110)的中點值為![]() =105)作為這組數據的平均分,據此,估計本次考試的平均分;
=105)作為這組數據的平均分,據此,估計本次考試的平均分;
(3)用分層抽樣的方法在分數段為[110,130)的學生中抽取一個容量為6的樣本,將該樣本看成一個總體,從中任取2人,求至多有1人在分數段[120,130)內的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com