Question

【題目】已知點A，B分別為橢圓E： 的左，右頂點，點P（0，﹣2），直線BP交E于點Q， 且△ABP是等腰直角三角形．
（Ⅰ）求橢圓E的方程；
（Ⅱ）設過點P的動直線l與E相交于M，N兩點，當坐標原點O位于以MN為直徑的圓外時，求直線l斜率的取值范圍．

Answer 1

【答案】解：（Ⅰ）由題意知：△ABP是等腰直角三角形，a=2，B（2，0），

設Q（x0，y0），由 ，則 ，

代入橢圓方程，解得b2=1，

∴橢圓方程為 ．

（Ⅱ）由題意可知，直線l的斜率存在，方程為y=kx﹣2，設M（x1，y1），N（x2，y2），

則 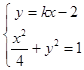，整理得：（1+4k2）x2﹣16kx+12=0，

由韋達定理可知：x1+x2= ，x1x2= ，

由直線l與E有兩個不同的交點，則△＞0，

即（﹣16k）2﹣4×12×（1+4k2）＞0，解得：k2＞ ，…①

由坐標原點O位于以MN為直徑的圓外，則 ，即x1x2+y1y2＞0，

則x1x2+y1y2=x1x2+（kx1﹣2）（kx2﹣2）

=（1+k2）x1x2﹣2k×（x1+x2）+4

=（1+k2） ﹣2k× +4＞0，

解得：k2＜4，…②

綜合①②可知： ＜k2＜4，解得 ＜k＜2或﹣2＜k＜﹣ ，

直線l斜率的取值范圍（﹣2，﹣ ）∪（ ，2）．

【解析】（Ⅰ）由題意可知：由 ，求得Q點坐標，即可求得橢圓E的方程；（Ⅱ）設直線y=kx﹣2，代入橢圓方程，由韋達定理，由△＞0，由坐標原點O位于以MN為直徑的圓外，則 ，由向量數量積的坐標公式，即可求得直線l斜率的取值范圍．