幾何證明選講如圖:已知圓上的弧
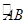
=
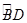
,過C點的圓的切線與BA的延長線交于E點
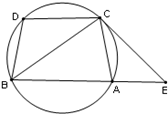
證明:(Ⅰ)∠ACE=∠BCD.(Ⅱ)BC
2=BE×CD.
由同圓中等圓弧的性質(zhì)可得∠ABC=∠BCD.由弦切角定理可得∠ACE=∠ABC,即可得出證明.(II)利用弦切角定理可得∠CDB=∠BCE,由相似三角形的判定定理可得△BEC∽△CBD,由相似三角形的性質(zhì)可得BC2=BE×CD.,即可求出BC
試題分析:解:(Ⅰ)因為
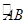
=
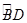
,
所以∠BCD=∠ABC.
又因為EC與圓相切于點C,
故∠ACE=∠ABC
所以∠ACE=∠BCD.(5分)
(Ⅱ)因為∠ECB=∠CDB,∠EBC=∠BCD,
所以△BDC~△ECB,
故BC:BE="CD:BC" .
即BC
2=BE×CD.(10分)
點評:熟練掌握同圓中等圓弧的性質(zhì)、弦切角定理、相似三角形的判定和性質(zhì)定理是解題的關(guān)鍵.
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
如圖,已知

與圓
相切于點

,直徑

,連結(jié)

交

于點

.
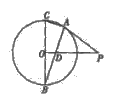
(1)求證:

;
(2)求證:
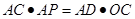
.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
直線

截圓x
2+y
2=4得的劣弧所對的圓心角是( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
若圓
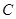
經(jīng)過坐標原點和點
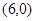
,且與直線
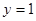
相切, 從圓
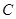
外一點
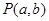
向該圓引切線
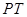
,
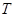
為切點,
(Ⅰ)求圓
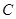
的方程;
(Ⅱ)已知點
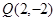
,且
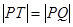
, 試判斷點
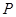
是否總在某一定直線
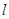
上,若是,求出
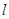
的方程;若不是,請說明理由;
(Ⅲ)若(Ⅱ)中直線
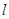
與
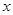
軸的交點為
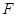
,點
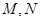
是直線
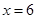
上兩動點,且以
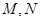
為直徑的圓
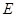
過點
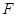
,圓
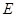
是否過定點?證明你的結(jié)論.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
如圖,

是⊙

的直徑,
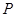
是

延長線上的一點,過
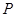
作⊙

的切線,切點為

,

,若

,則⊙

的直徑


查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
已知
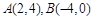
,則以
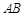
為直徑的圓的方程是( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
若直線3x-4y+12=0與兩坐標軸的交點為A,B,則以線段AB為直徑的圓的方程為____________________。
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
當
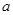
為任意實數(shù)時,直線
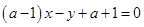
恒過定點
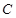
,則以
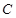
為圓心,半徑為
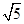
的圓是( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
如圖所示,已知點P是⊙O外一點,PS、PT是⊙O的兩條切線,過點P作⊙O
的割線PAB,交⊙O于A、B兩點,與ST交于點C,求證:


查看答案和解析>>

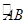 =
=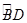 ,過C點的圓的切線與BA的延長線交于E點
,過C點的圓的切線與BA的延長線交于E點
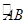 =
=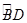 ,
,

 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案 經(jīng)過坐標原點和點
經(jīng)過坐標原點和點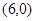 ,且與直線
,且與直線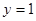 相切, 從圓
相切, 從圓 外一點
外一點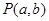 向該圓引切線
向該圓引切線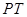 ,
,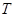 為切點,
為切點,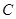 的方程;
的方程;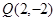 ,且
,且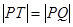 , 試判斷點
, 試判斷點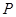 是否總在某一定直線
是否總在某一定直線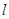 上,若是,求出
上,若是,求出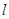 的方程;若不是,請說明理由;
的方程;若不是,請說明理由;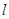 與
與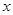 軸的交點為
軸的交點為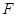 ,點
,點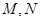 是直線
是直線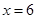 上兩動點,且以
上兩動點,且以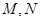 為直徑的圓
為直徑的圓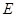 過點
過點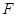 ,圓
,圓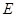 是否過定點?證明你的結(jié)論.
是否過定點?證明你的結(jié)論. 
