Question

【題目】在如圖所示的空間幾何體中，平面ACD⊥平面ABC，△ACD與△ACB是邊長為2的等邊三角形，BE=2，BE和平面ABC所成的角為60°，且點E在平面ABC上的射影落在的平分線上.

（1）求證：DE∥平面ABC；

（2）求此空間幾何體的體積.

Answer 1

【答案】（1）詳見解析；（2）.

【解析】

試題分析：（1）要證明線面平行，即先證明線線平行，取AC中點O，連接BO，DO，則BO⊥AC，DO⊥AC，作EF⊥平面ABC，根據題意，點F落在BO上，∴EBF=60°，易求得，這樣就可證明,且,所以四邊形是平行四邊形，得到;（2）將幾何體的體積分割為兩個三棱錐的體積，即,根據所給的數據代入得到結果.

試題解析：（1）由題意知，△ABC，△ACD都是邊長為2的等邊三角形，取AC中點O，連接BO，DO，則BO⊥AC，DO⊥AC，

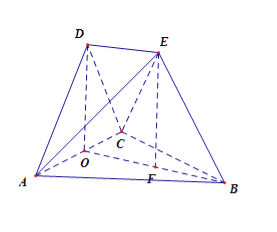
又∵平面ACD⊥平面ABC，∴DO⊥平面ABC，作EF⊥平面ABC，那么EF∥DO，根據題意，點F落在BO上，∴EBF=60°，易求得，

∴四邊形DEFO是平行四邊形，∴DE∥OF，DE平面ABC，OF平面ABC，

∴DE∥平面ABC.

（2）由（1）：BO⊥AC，平面ACD⊥平面ABC且交線為AC，

∴BO⊥平面ACD，∴DE⊥平面ACD，

∴三棱錐E-ACD的體積

，

三棱錐E-ACB的體積，

∴此空間幾何體的體積.