【題目】已知中心在原點，焦點在x軸上的橢圓的一個頂點坐標為（0，1），其離心率為 
（1）求橢圓的標準方程；
（2）橢圓上一點P滿足∠F1PF2=60°，其中F1 ， F2為橢圓的左右焦點，求△F1PF2的面積．
【答案】
（1）
解：設橢圓的標準方程為 
（a＞b＞0），
橢圓的一個頂點為（0，1）則b=1，
由橢圓的離心率e= 
= 
= 
，解得：a2=3，
橢圓的標準方程為 
（2）
解：設丨PF1丨=n，丨PF2丨=m，∠F1PF2=60°，
由余弦定理可知：丨F1F2丨2=丨PF1丨2+丨PF2丨2﹣2丨PF1丨丨PF1丨cos60°，
4c2=m2+n2﹣2mncos60°=（m+n）2﹣3mn=4a2﹣3mn，
則4×（ 
）2=4a2﹣3mn，解得：mn= 
，
即丨PF1丨丨PF1丨= ，
△F1PF2的面積S= 
×丨PF1丨丨PF1丨×sin∠F1PF2，
∴ 
，
△F1PF2的面積 
【解析】（1）設橢圓的方程，則b=1，根據橢圓的離心率即可求得a的值，即可求得橢圓方程；（2）根據余弦定理，即可求得丨PF1丨丨PF1丨，利用三角形的面積公式即可求得△F1PF2的面積．
直通貴州名校周測月考直通名校系列答案科目：高中數學 來源： 題型：
【題目】（文科做）已知函數f（x）=x﹣ 
﹣（a+2）lnx，其中實數a≥0．
（1）若a=0，求函數f（x）在x∈[1，3]上的最值；
（2）若a＞0，討論函數f（x）的單調性．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司為確定下一年度投入某種產品的宣傳費，需了解年宣傳費
（單位:千元)對年銷售量
（單位: 
)和年利潤
（單位:千元)的影響.對近8年的年宣傳費
和年銷售量
數據作了初步處理，得到下面的散點圖及一些統計量的值.
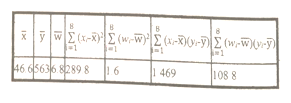
表中
.
（1）根據散點圖判斷
與
哪一個適宜作為年銷售量
關于年宣傳費
的回歸類型？（給出判斷即可，不必說明理由）
（2）根據（1）的判斷結果及表中數據，建立
關于
的回歸方程；
（3）已知這種產品的利潤
與
的的關系為
.根據（2）的結果回答下列問題：
（ⅰ）年宣傳費
時，年銷售量及年利潤的預報值是多少？
（ⅱ）年宣傳費
為何值時，年利潤的預報值最大？
附:對于一組數據
，其回歸直線
的的斜率和截距的最小二乘估計為
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，有一塊半徑長為1米的半圓形鋼板，現要從中截取一個內接等腰 梯形部件ABCD，設梯形部件ABCD的面積為
平方米．
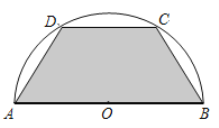
（1）按下列要求寫出函數關系式：
①設
（米），將表示成
的函數關系式；
②設
，將表示成
的函數關系式．
（2）求梯形部件ABCD面積的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}是首項為正數的等差數列，a1a2=3，a2a3=15．
（1）求數列{an}的通項公式；
（2）設bn=（an+1）2 
，求數列{bn}的前n項和Tn ．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
