
如圖,公園有一塊邊長為2的等邊△ABC的邊角地,現(xiàn)修成草坪, 圖中DE把草坪分成面積相等的兩部分,D在AB上,E在AC上.
(1)設(shè) (x≥0),
(x≥0), ,求用
,求用 表示
表示 的函數(shù)關(guān)系式,并求函數(shù)的定義域;
的函數(shù)關(guān)系式,并求函數(shù)的定義域;
(2).如果 是灌溉水管,為節(jié)約成本,希望它最短,
是灌溉水管,為節(jié)約成本,希望它最短, 的位置應(yīng)在哪里?如果
的位置應(yīng)在哪里?如果 是參觀線路,則希望它最長,
是參觀線路,則希望它最長, 的位置又應(yīng)在哪里?請予證明.
的位置又應(yīng)在哪里?請予證明.
(1) 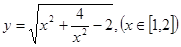
(2) 如果 是水管,當(dāng)
是水管,當(dāng)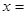
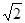 時,
時, 
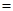
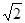 最短.
最短.
如果 是參觀線路,則
是參觀線路,則 為
為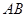 中線或
中線或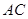 中線時,
中線時, 最長
最長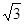 .
.
解析試題分析:(1)顯然變量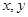 都在
都在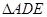 中,尋找兩邊的關(guān)系,利用余弦定理即可.但是發(fā)現(xiàn)還有邊
中,尋找兩邊的關(guān)系,利用余弦定理即可.但是發(fā)現(xiàn)還有邊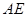 存在,所以得尋找
存在,所以得尋找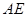 .根據(jù)面積相等,利用面積公式即可得到
.根據(jù)面積相等,利用面積公式即可得到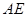 與
與 的關(guān)系.消掉
的關(guān)系.消掉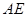 即可得到解析式.但是要考慮實(shí)際意義,即函數(shù)的定義域.
即可得到解析式.但是要考慮實(shí)際意義,即函數(shù)的定義域.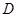 在
在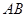 上,可知自變量的范圍是
上,可知自變量的范圍是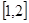 .
.
(2) 如果 是水管,根據(jù)(1)中的解析式,觀察形式,可知利用均值不等式即可求得最小值.
是水管,根據(jù)(1)中的解析式,觀察形式,可知利用均值不等式即可求得最小值.
如果 是參觀線路,則要求其盡可能的長,所以分析函數(shù)的單調(diào)性求最大值即可.
是參觀線路,則要求其盡可能的長,所以分析函數(shù)的單調(diào)性求最大值即可.
(1)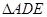 中,根據(jù)余弦定理有
中,根據(jù)余弦定理有
即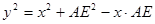 ; ①
; ①
又 ,即
,即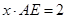 .②
.②
②代入①得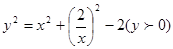 , ∴
, ∴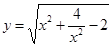
由題意知點(diǎn)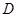 至少是
至少是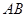 的中點(diǎn),
的中點(diǎn), 才能把草坪分成面積相等的兩部分。
才能把草坪分成面積相等的兩部分。
所以 ,又
,又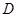 在
在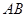 上,
上,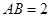 ,所以函數(shù)的定義域是
,所以函數(shù)的定義域是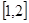 ,
,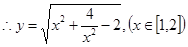 .
.
(2)如果 是水管
是水管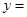
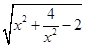
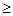
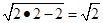 ,
,
當(dāng)且僅當(dāng)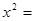
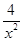 ,即
,即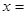
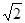 時“=”成立,故
時“=”成立,故 ∥
∥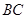 ,且
,且
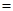
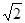 .
.
如果 是參觀線路,記
是參觀線路,記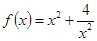 ,可知
,可知
函數(shù)在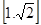 上遞減,在
上遞減,在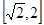 上遞增,
上遞增,
故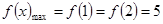 所以
所以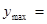
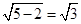 .
.
即 為
為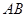 中線或
中線或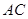 中線時,
中線時, 最長。
最長。
考點(diǎn):實(shí)際應(yīng)用題;余弦定理;利用均值不等式求函數(shù)的最小值;利用函數(shù)的單調(diào)性得函數(shù)的最大值.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
在△ABC中,內(nèi)角A,B,C所對的邊分別為a,b,c,已知sin B(tan A+tan C)=tan Atan C.
(1)求證:a,b,c成等比數(shù)列;
(2)若a=1,c=2,求△ABC的面積S.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
△ABC中,a、b、c分別是角A、B、C的對邊,△ABC的周長為 +2,且sinA+sinB=
+2,且sinA+sinB= sinC.(1)求邊c的長. (2)若△ABC的面積為
sinC.(1)求邊c的長. (2)若△ABC的面積為 sinC,求角C的度數(shù).
sinC,求角C的度數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
在△ABC中,角A,B,C的對邊分別為 ,且A,B,C成等差數(shù)列。
,且A,B,C成等差數(shù)列。
(1)若 ,
, ,求△ABC的面積;
,求△ABC的面積;
(2)若 成等比數(shù)列,試判斷△ABC的形狀。
成等比數(shù)列,試判斷△ABC的形狀。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,在△ABC中,B= ,AC=2
,AC=2 ,cosC=
,cosC= .
.
(1)求sin∠BAC的值;
(2)設(shè)BC的中點(diǎn)為D,求中線AD的長.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com