Question

【題目】2014年“五一節”期間，高速公路車輛較多，交警部門通過路面監控裝置抽樣調查某一山區路段汽車行駛速度，采用的方法是：按到達監控點先后順序，每隔50輛抽取一輛，總共抽取120輛，分別記下其行車速度，將行車速度（km/h）分成七段[60，65），[65，70），[70，75），[75，80），[80，85），[85，90），[90，95）后得到如圖所示的頻率分布直方圖，據圖解答下列問題：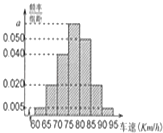

（1）求a的值，并說明交警部門采用的是什么抽樣方法？
（2）求這120輛車行駛速度的眾數和中位數的估計值（精確到0.1）；
（3）若該路段的車速達到或超過90km/h即視為超速行駛，試根據樣本估計該路段車輛超速行駛的概率．

Answer 1

【答案】
（1）解：由頻率分布直方圖知：（a+0.05+0.04+0.02+0.02+0.005+0.005）×5=1，

∴a=0.06，

該抽樣方法是系統抽樣；

（2）解：根據眾數是最高矩形底邊中點的橫坐標，∴眾數為77.5；

∵前三個小矩形的面積和為0.005×5+0.020×5+0.040×5=0.325，

第四個小矩形的面積為0.06×5=0.3，

∴中位數在第四組，設中位數為75+x，則0.325+0.06×x=0.5x≈2.9，

∴數據的中位數為77.9；

（3）解：樣本中車速在[90，95）有0.005×5×120=3（輛），

∴估計該路段車輛超速的概率P= = ．

【解析】（1）根據頻率分布直方圖中所有矩形的面積和為1求得a值，根據相同抽樣方法的特征判斷其抽樣方法；（2）根據眾數是最高矩形底邊中點的橫坐標求眾數；根據中位數是從左數小矩形面積和為0.5的矩形底邊上點的橫坐標求中位數；（3）利用直方圖求出樣本中車速在[90，95）頻數，利用個數比求超速車輛的概率．
【考點精析】解答此題的關鍵在于理解平均數、中位數、眾數的相關知識，掌握⑴平均數、眾數和中位數都是描述一組數據集中趨勢的量；⑵平均數、眾數和中位數都有單位；⑶平均數反映一組數據的平均水平，與這組數據中的每個數都有關系，所以最為重要，應用最廣；⑷中位數不受個別偏大或偏小數據的影響；⑸眾數與各組數據出現的頻數有關，不受個別數據的影響，有時是我們最為關心的數據．