
【題目】已知函數![]() 在區間
在區間![]() 上有最大值3和最小值
上有最大值3和最小值![]() .
.
(1)求實數![]() 的值;
的值;
(2)設![]() ,若不等式
,若不等式![]() 在
在![]() 上恒成立,求實數
上恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1) ![]() .(2)
.(2) ![]() .
.
【解析】試題分析:(1)根據二次函數的性質求出![]() 的單調區間,求出函數的最大值和最小值,得到關于
的單調區間,求出函數的最大值和最小值,得到關于![]() 的方程組,解出即可;(2)問題轉化為
的方程組,解出即可;(2)問題轉化為![]() ,令
,令![]() ,根據函數的單調性求出
,根據函數的單調性求出![]() 的最小值,求出
的最小值,求出![]() 的范圍即.
的范圍即.
試題解析:(1)∵![]() 的對稱軸是
的對稱軸是![]() ,又∵
,又∵![]() .
.
∴![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增;
上單調遞增;
∴當![]() 時,
時, ![]() 取最小值
取最小值![]() ,當
,當![]() 時,
時, ![]() 取最大值3;
取最大值3;
即![]() ,解得
,解得![]() .
.
(2)∵![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
令![]() ,則
,則![]() 在
在![]() 上是增函數,
上是增函數,
故![]() ,
,
∴![]() 在
在![]() 上恒成立時,
上恒成立時, ![]() .
.
【方法點晴】本題主要考查二次函數的最值以及不等式恒成立問題,屬于難題.不等式恒成立問題常見方法:① 分離參數![]() 恒成立(
恒成立(![]() 可)或
可)或![]() 恒成立(
恒成立(![]() 即可);② 數形結合(
即可);② 數形結合(![]() 圖象在
圖象在![]() 上方即可);③ 討論最值
上方即可);③ 討論最值![]() 或
或![]() 恒成立;④ 討論參數.本題是利用方法 ① 求得
恒成立;④ 討論參數.本題是利用方法 ① 求得![]() 的范圍的.
的范圍的.


科目:高中數學 來源: 題型:
【題目】如圖所示,正方體![]() 的棱長為1,
的棱長為1, ![]() ,
, ![]() 分別是棱
分別是棱![]() ,
, ![]() 的中點,過直線
的中點,過直線![]() 的平面分別與棱
的平面分別與棱![]() ,
, ![]() 交于
交于![]() ,
, ![]() ,設
,設![]() ,
, ![]() ,給出以下命題:
,給出以下命題:
①四邊形![]() 為平行四邊形;
為平行四邊形;
②若四邊形![]() 面積
面積![]() ,
, ![]() ,則
,則![]() 有最小值;
有最小值;
③若四棱錐![]() 的體積
的體積![]() ,
, ![]() ,則
,則![]() 為常函數;
為常函數;
④若多面體![]() 的體積
的體積![]() ,
, ![]() ,則
,則![]() 為單調函數.
為單調函數.
⑤當![]() 時,四邊形
時,四邊形![]() 為正方形.
為正方形.
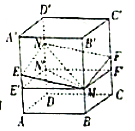
其中假命題的個數為( )
A. 0 B. 3 C. 2 D. 1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】張師傅想要一個如圖1所示的鋼筋支架的組合體,來到一家鋼制品加工店定制,拿出自己畫的組合體三視圖(如圖2所示).店老板看了三視圖,報了最低價,張師傅覺得很便宜,當即甩下定金和三視圖,約定第二天提貨.第二天提貨時,店老板一臉壞笑的捧出如圖3–1所示的組合體,張師傅一看,臉都綠了:“奸商,怎能如此偷工減料”.店老板說,我是按你的三視圖做的,要不我給你加一個正方體,但要加價,隨機加上了一個正方體,得到如圖3–2所示的組合體;張師傅臉還是綠的,店老板又加上一個正方體,組成了如圖 3–3 所示的組合體,又加價;張師傅臉繼續綠,店老板再加一個正方體,組成如圖 3–4 所示的組合體,再次加價;雙方就三視圖爭吵不休……
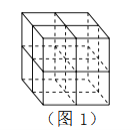
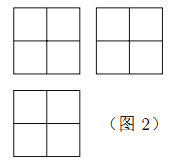
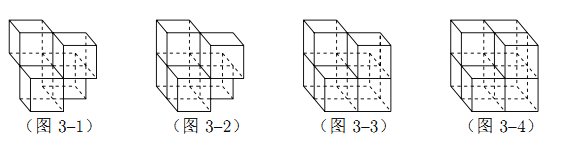
你認為店老板提供的![]() 個組合體的三視圖與張師傅畫的三視圖一致的個數是( )
個組合體的三視圖與張師傅畫的三視圖一致的個數是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位實行休年假制度三年以來,50名職工休年假的次數進行的調查統計結果如下表所示:
休假次數 | 0 | 1 | 2 | 3 |
人數 | 5 | 10 | 20 | 15 |
根據表中信息解答以下問題:
(1)從該單位任選兩名職工,求這兩人休年假次數之和為4的概率;
(2)從該單位任選兩名職工,用![]() 表示這兩人休年假次數之差的絕對值,求隨機變量
表示這兩人休年假次數之差的絕對值,求隨機變量![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】空氣污染,又稱為大氣污染,是指由于人類活動或自然過程引起某些物質進入大氣中,呈現出足夠的濃度,達到足夠的時間,并因此危害了人體的舒適、健康和福利或環境的現象.全世界也越來越關注環境保護問題.當空氣污染指數(單位:μg/m3)為0~50時,空氣質量級別為一級,空氣質量狀況屬于優;當空氣污染指數為50~100時,空氣質量級別為二級,空氣質量狀況屬于良;當空氣污染指數為100~150時,空氣質量級別為三級,空氣質量狀況屬于輕度污染;當空氣污染指數為150~200時,空氣質量級別為四級,空氣質量狀況屬于中度污染;當空氣污染指數為200~300時,空氣質量級別為五級,空氣質量狀況屬于重度污染;當空氣污染指數為300以上時,空氣質量級別為六級,空氣質量狀況屬于嚴重污染.2017年1月某日某省x個監測點數據統計如下:
空氣污染指數 (單位:μg/m3) |
|
|
|
|
監測點個數 | 15 | 40 | y | 10 |
(1)根據所給統計表和頻率分布直方圖中的信息求出x,y的值,并完成頻率分布直方圖;
(2)若A市共有5個監測點,其中有3個監測點為輕度污染,2個監測點為良.從中任意選取2個監測點,事件A“其中至少有一個為良”發生的概率是多少?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,橢圓
,橢圓![]() 的離心率為
的離心率為![]() 是橢圓的焦點,直線
是橢圓的焦點,直線![]() 的斜率為
的斜率為![]() 為坐標原點.
為坐標原點.
(1)求橢圓![]() 的方程;
的方程;
(2)設過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,當
兩點,當![]() 的面積最大時,求直線
的面積最大時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解甲、乙兩個班級某次考試的數學成績(單位:分),從甲、乙兩個班級中分別隨機抽取5名學生的成績作樣本,如圖是樣本的莖葉圖.規定:成績不低于120分時為優秀成績.

(1)從甲班的樣本中有放回的隨機抽取 2 個數據,求其中只有一個優秀成績的概率;
(2)從甲、乙兩個班級的樣本中分別抽取2名同學的成績,記獲優秀成績的人數為![]() ,求
,求![]() 的分布列和數學期望
的分布列和數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在心理學研究中,常采用對比試驗的方法評價不同心理暗示對人的影響,具體方法如下:將參加試驗的志愿者隨機分成兩組,一組接受甲種心理暗示,另一組接受乙種心理暗示,通過對比這兩組志愿者接受心理暗示后的結果來評價兩種心理暗示的作用,現有5名男志愿![]() 和3名女志愿者
和3名女志愿者![]() ,從中隨機抽取4人接受甲種心理暗示,另4人接受乙種心理暗示.
,從中隨機抽取4人接受甲種心理暗示,另4人接受乙種心理暗示.
(1)求接受甲種心理暗示的志愿者中包含![]() 但不包含
但不包含![]() 的頻率.
的頻率.
(2)用![]() 表示接受乙種心理暗示的女志愿者人數,求
表示接受乙種心理暗示的女志愿者人數,求![]() 的分布列與數學期望
的分布列與數學期望![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設某物體一天中的溫度![]() 是時間
是時間![]() 的函數,已知
的函數,已知![]() ,其中溫度的單位是
,其中溫度的單位是![]() ,時間的單位是小時,規定中午12:00相應的
,時間的單位是小時,規定中午12:00相應的![]() ,中午12:00以后相應的
,中午12:00以后相應的![]() 取正數,中午12:00以前相應的
取正數,中午12:00以前相應的![]() 取負數(例如早上8:00相應的
取負數(例如早上8:00相應的![]() ,下午16:00相應的
,下午16:00相應的![]() ),若測得該物體在中午12:00的溫度為
),若測得該物體在中午12:00的溫度為![]() ,在下午13:00的溫度為
,在下午13:00的溫度為![]() ,且已知該物體的溫度在早上8:00與下午16:00有相同的變化率.
,且已知該物體的溫度在早上8:00與下午16:00有相同的變化率.
(1)求該物體的溫度![]() 關于時間
關于時間![]() 的函數關系式;
的函數關系式;
(2)該物體在上午10:00至下午14:00這段時間中(包括端點)何時溫度最高?最高溫度是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com