
【題目】已知函數![]() .
.
⑴求函數![]() 的單調區間;
的單調區間;
⑵如果對于任意的![]() ,
,![]() 總成立,求實數
總成立,求實數![]() 的取值范圍.
的取值范圍.
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 是邊長為2的正方形,
是邊長為2的正方形,![]() ,且
,且![]() ,
,![]() 為
為![]() 中點.
中點.
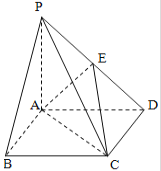
(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)在線段![]() 上是否存在點
上是否存在點![]() ,使得點
,使得點![]() 到平
到平
面![]() 的距離為
的距離為![]() ?若存在,確定點
?若存在,確定點![]() 的位置;
的位置;
若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】根據某鎮家庭抽樣調查的統計,2003年每戶家庭平均消費支出總額為1萬元,其中食品消費額為0.6萬元.預測2003年后,每戶家庭平均消費支出總額每年增加3000元,如果到2005年該鎮居民生活狀況能達到小康水平(即恩格爾系數n滿足![]() ),則這個鎮每戶食品消費額平均每年的增長率至多是多少(精確到0.1%)?
),則這個鎮每戶食品消費額平均每年的增長率至多是多少(精確到0.1%)?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x-a|-1,(a為常數).
(1)若f(x)在x∈[0,2]上的最大值為3,求實數a的值;
(2)已知g(x)=xf(x)+a-m,若存在實數a∈(-1,2],使得函數g(x)有三個零點,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合M是具有下列性質的函數![]() 的全體:存在實數對
的全體:存在實數對![]() ,使得
,使得![]() 對定義域內任意實數x都成立.
對定義域內任意實數x都成立.
(1)判斷函數![]() ,
,![]() 是否屬于集合
是否屬于集合![]() ;
;
(2)若函數![]() 具有反函數
具有反函數![]() ,是否存在相同的實數對
,是否存在相同的實數對![]() ,使得
,使得![]() 與
與![]() 同時屬于集合
同時屬于集合![]()
![]() 若存在,求出相應的
若存在,求出相應的![]() ;若不存在,說明理由;
;若不存在,說明理由;
(3)若定義域為![]() 的函數
的函數![]() 屬于集合
屬于集合![]() ,且存在滿足有序實數對
,且存在滿足有序實數對![]() 和
和![]() ;當
;當![]() 時,
時,![]() 的值域為
的值域為![]() ,求當
,求當![]() 時函數
時函數![]() 的值域.
的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校舉行聯歡會,所有參演的節目都由甲、乙、丙三名專業老師投票決定是否獲獎.甲、乙、丙三名老師都有“獲獎”、“待定”、“淘汰”三類票各一張,每個節目投票時,甲、乙、丙三名老師必須且只能投一張票,每人投三類票中的任何一類票的概率都為![]() ,且三人投票相互沒有影響.若投票結果中至少有兩張“獲獎”票,則決定該節目最終獲一等獎;否則,該節目不能獲一等獎.
,且三人投票相互沒有影響.若投票結果中至少有兩張“獲獎”票,則決定該節目最終獲一等獎;否則,該節目不能獲一等獎.
(1)求某節目的投票結果是最終獲一等獎的概率;
(2)求該節目投票結果中所含“獲獎”和“待定”票票數之和X的分布列及均值和方差.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com