Question

【題目】已知函數f（x）=1﹣ （a＞0且a≠1）是定義在R上的奇函數．
（1）求a的值；
（2）求f（x）的值域；
（3）若關于x的方程|f（x）（2x+1）|=m有1個實根，求實數m的取值范圍；
（4）當x∈（0，1]時，tf（x）≥2x﹣2恒成立，求實數t取值范圍．

Answer 1

【答案】
（1）解：∵函數f（x）=1﹣ （a＞0且a≠1）是定義在R上的奇函數，

∴f（﹣x）=﹣f（x），解得：a=2

（2）解： ，

∴y∈（﹣1，1）

（3）解：設h（x）=|2x﹣1|，g（x）=m，

作圖，如圖示：

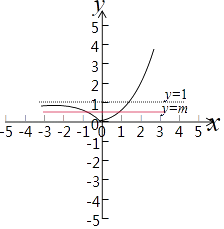
如圖當m≥1時，h（x）=|2x﹣1|與g（x）=m有一個交點，

所以|f（x）（2x+1）|=m有一個實根，

所以m∈[1，+∞）∪{0}

（4）解： （2x）2﹣（t+1）2x+t﹣2≤0，

令2x=u，x∈（0，1]u∈（1，2]，

u∈（1，2]時，u2﹣（t+1）u+t﹣2≤0恒成立，

則

【解析】（1）根據函數的奇偶性得到f（﹣x）=﹣f（x），求出a的值即可；（2）將f（x）變形，解關于y的不等式，求出f（x）的值域即可；（3）結合圖象求出m的范圍即可；（4）令2x=u，x∈（0，1]u∈（1，2]，得到u∈（1，2]時，u2﹣（t+1）u+t﹣2≤0恒成立，求出t的范圍即可．