Question

【題目】在等腰梯形ABCD中，AB∥CD，且|AB|=2，|AD|=1，|CD|=2x其中x∈（0，1），以A，B為焦點且過點D的雙曲線的離心率為e1 ， 以C，D為焦點且過點A的橢圓的離心率為e2 ， 若對任意x∈（0，1）不等式t＜e1+e2恒成立，則t的最大值為（ ）
A.
B.
C.2
D.

Answer 1

【答案】B
【解析】解：在等腰梯形ABCD中，BD2=AD2+AB2﹣2ADABcos∠DAB
=1+4﹣2×1×2×（1﹣x）=1+4x，
由雙曲線的定義可得a1= ，c1=1，e1= ，
由橢圓的定義可得a2= ，c2=x，e2= ，
則e1+e2= + = + ，
令t= ∈（0， ﹣1），
則e1+e2= （t+ ）在（0， ﹣1）上單調遞減，
所以e1+e2＞ ×（ ﹣1+ ）= ，
故選：B．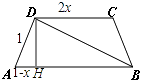

根據余弦定理表示出BD，進而根據雙曲線的定義可得到a1的值，再由AB=2c1 ， e= 可表示出e1 ， 同樣的在橢圓中用c2和a2表示出e2 ， 然后利用換元法即可求出e1+e2的取值范圍，即得結論